\(lim_{n→∞} \frac1{2^n}(\frac1{\sqrt{1-1/2^n}} +\frac1{\sqrt{1-\frac2{2^n}}}+\frac1{\sqrt{1-\frac3{2^n}}}+...+\frac1{\sqrt{1-\frac{2^n-1}{2^n}}})\) is equal to
\(\frac1{2}\)
1
2
-2
The Correct Option is C
Solution and Explanation
\(I =lim_{n→∞} \frac1{2^n}(\frac1{\sqrt{1-1/2^n}} +\frac1{\sqrt{1-\frac2{2^n}}}+\frac1{\sqrt{1-\frac3{2^n}}}+...+\frac1{\sqrt{1-\frac{2^n-1}{2^n}}})\)
Let \(2^n=t \) and if\( n→∞\) then \(t→∞ \)
\(I= lim_{n→∞} \frac1{t} (\overset{t=1}{\underset{r=1}\sum} \frac1{√1-\frac{r}{t}})\)
\(l= ∫_0 ^1 \frac{dx}{√1-x}=∫_0^1 \frac {dx}{\sqrt {x}} \) \(\bf{∫_0^a f(x)dx=∫_0^a f(a-x)dx }\)
\(=[2x^{\frac1{2}}]^1_0 \)
\(=2\)
Top Questions on Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- If $\frac{x+3}{(x+1)(x^2+2)} = \frac{a}{x+1} + \frac{bx+c}{x^2+2}$ then $a-b+c =$
- TS EAMCET - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- Let \( \alpha_1 \) and \( \beta_1 \) be the distinct roots of \( 2x^2 + (\cos\theta)x - 1 = 0, \ \theta \in (0, 2\pi) \). If \( m \) and \( M \) are the minimum and the maximum values of \( \alpha_1 + \beta_1 \), then \( 16(M + m) \) equals:
- JEE Main - 2025
- Maxima and Minima
- Let the line \( x + y = 1 \) meet the circle \( x^2 + y^2 = 4 \) at the points A and B. If the line perpendicular to AB and passing through the midpoint of the chord AB intersects the circle at C and D, then the area of the quadrilateral ABCD is equal to:
- JEE Main - 2025
- Coordinate Geometry
- The number of different 5 digit numbers greater than 50000 that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, 7, such that the sum of their first and last digits should not be more than 8, is:
- JEE Main - 2025
- permutations and combinations
- Two concave refracting surfaces of equal radii of curvature and refractive index 1.5 face each other in air as shown in figure. A point object O is placed midway, between P and B. The separation between the images of O, formed by each refracting surface is:

A symmetric thin biconvex lens is cut into four equal parts by two planes AB and CD as shown in the figure. If the power of the original lens is 4D, then the power of a part of the divided lens is:

Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
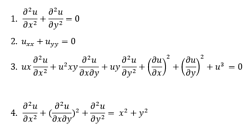
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
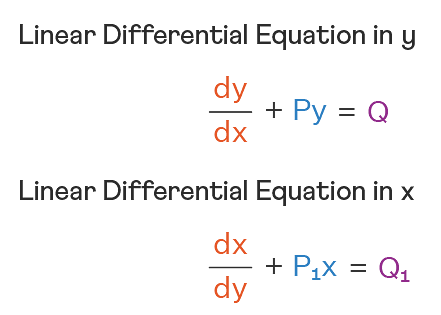
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations