Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- 483
- 528
- 575
- 624
The Correct Option is B
Approach Solution - 1
(an+2−an+1)−2(an+1−an)−1=0|
Put n = 0
(a2−a1)−2(a1−a0)−1=0
n = 1
(a3−a2)−2(a2−a1)−1=0
n = 2
(a4−a3)−2(a3−a2)−1=0
n=n
(an+2–an+1)−2(an+1−an)−1=0
On adding,
(an+2–a1)−2(aa+1−a0)−(n+1)=0
∴an+2−2an+1−(n+1)=0
n\(\rightarrow\)n–2
an–2an−1−n+1=0
Now,
a25a23−2a25a22−2a23a24+4a22a24
=a25(a23−2a22)−2a24(a23−2a22)
=(a25−2a24)(a23−2a22)
=24⋅22
=528
So, the correct option is (B): 528
Approach Solution -2
Consider the sequence \( \{a_n\}_{n=0}^{\infty} \) defined by the recurrence relation:
\( a_{n+2} - 3a_{n+1} + 2a_n = 1, \quad a_0 = a_1 = 0 \)
Step 1: Solve the Homogeneous Equation
The homogeneous part of the recurrence is:
\( a_{n+2} - 3a_{n+1} + 2a_n = 0 \)
Its characteristic equation is:
\( r^2 - 3r + 2 = 0 \)
Factoring, we get:
\( (r - 1)(r - 2) = 0 \)
Hence, the roots are \( r = 1 \) and \( r = 2 \), and the general solution of the homogeneous equation is:
\( a_n^{(h)} = A + B \cdot 2^n \)
Step 2: Find a Particular Solution
Since the non-homogeneous term is a constant (1), we try a particular solution of the form:
\( a_n^{(p)} = C \cdot n \)
Substituting into the recurrence, we have:
\( C(n+2) - 3C(n+1) + 2Cn = Cn + 2C - 3Cn - 3C + 2Cn = -C \)
Setting \( -C = 1 \) gives \( C = -1 \). Thus, the particular solution is:
\( a_n^{(p)} = -n \)
Step 3: General Solution and Initial Conditions
The general solution is the sum of the homogeneous and particular solutions:
\( a_n = A + B \cdot 2^n - n \)
Using the initial conditions:
- For \( n = 0 \): \( a_0 = A + B = 0 \)
- For \( n = 1 \): \( a_1 = A + 2B - 1 = 0 \)
Subtracting the first equation from the second yields:
\( (A+2B) - (A+B) = B = 1 \)
Therefore, \( A = -1 \), and the closed-form expression for the sequence is:
\( a_n = 2^n - n - 1 \)
Step 4: Evaluate the Expression
We wish to compute:
\( E = a_{25}a_{23} - 2a_{25}a_{22} - 2a_{23}a_{24} + 4a_{22}a_{24} \)
Notice that this expression factors as:
\( E = \bigl(a_{25} - 2a_{24}\bigr)\bigl(a_{23} - 2a_{22}\bigr) \)
Let’s simplify the term \( a_n - 2a_{n-1} \) using the closed form:
\( a_n - 2a_{n-1} = \Bigl(2^n - n - 1\Bigr) - 2\Bigl(2^{n-1} - (n-1) - 1\Bigr) \)
Expanding, we get:
\( = 2^n - n - 1 - 2^n + 2(n-1) + 2 = n - 1 \)
Therefore:
- For \( n = 25 \): \( a_{25} - 2a_{24} = 25 - 1 = 24 \)
- For \( n = 23 \): \( a_{23} - 2a_{22} = 23 - 1 = 22 \)
Thus, the expression simplifies to:
\( E = 24 \times 22 = 528 \)
Final Answer
The value of the expression is 528.
Top Questions on Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- If $\frac{x+3}{(x+1)(x^2+2)} = \frac{a}{x+1} + \frac{bx+c}{x^2+2}$ then $a-b+c =$
- TS EAMCET - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of the integral: ∫ (2x + 3)/((xy)(x^2 + 1)) dx
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- The area of the region enclosed by the curves \( y = x^2 - 4x + 4 \) and \( y^2 = 16 - 8x \) is:
- JEE Main - 2025
- Area between Two Curves
- 2.8 \( \times 10^{-3} \) mol of \( \text{CO}_2 \) is left after removing \( 10^{21} \) molecules from its ‘\( x \)’ mg sample. The mass of \( \text{CO}_2 \) taken initially is: Given: \( N_A = 6.02 \times 10^{23} \, \text{mol}^{-1} \)
- JEE Main - 2025
- Mole concept and Molar Masses
- A conducting bar moves on two conducting rails as shown in the figure. A constant magnetic field \( B \) exists into the page. The bar starts to move from the vertex at time \( t = 0 \) with a constant velocity. If the induced EMF is \( E \propto t^n \), then the value of \( n \) is ________________________.

- JEE Main - 2025
- Electromagnetic induction

In the first configuration (1) as shown in the figure, four identical charges \( q_0 \) are kept at the corners A, B, C and D of square of side length \( a \). In the second configuration (2), the same charges are shifted to mid points C, E, H, and F of the square. If \( K = \frac{1}{4\pi \epsilon_0} \), the difference between the potential energies of configuration (2) and (1) is given by:
- JEE Main - 2025
- Electromagnetic Field (EMF)
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
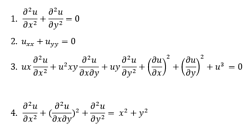
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
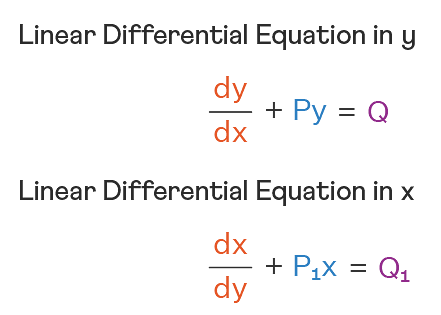
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations