The electric potential at the center of two concentric half rings of radii $R_1$ and $R_2$, having same linear charge density $\lambda$ is :
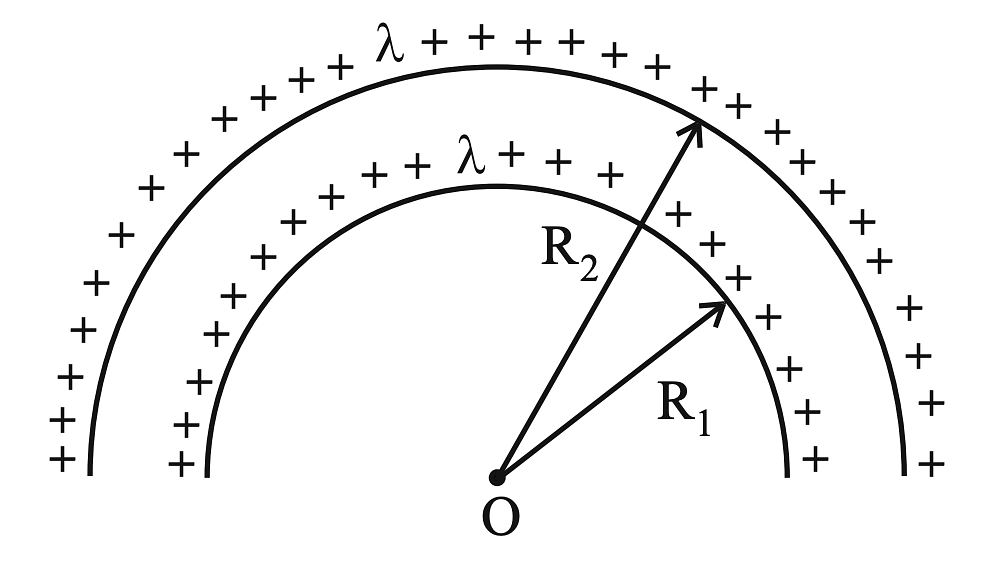

- $\frac{2 \lambda}{\epsilon_0}$
- $\frac{\lambda}{2 \epsilon_0}$
- $\frac{\lambda}{4 \epsilon_0}$
- $\frac{\lambda}{\epsilon_0}$
The Correct Option is B
Approach Solution - 1
The potential at the center due to a half ring is given by:
\[ V = \frac{\lambda \cdot \pi R}{4 \pi \epsilon_0 R} = \frac{\lambda}{4 \epsilon_0} \]
For two concentric half rings:
\[ V_{\text{total}} = \frac{\lambda}{4 \epsilon_0} + \frac{\lambda}{4 \epsilon_0} = \frac{\lambda}{2 \epsilon_0} \]
Thus, the correct answer is \( \frac{\lambda}{2 \epsilon_0} \).
Approach Solution -2
Potential at centre
Top Questions on Gauss Law
- If the net flux through a cube is 1.05 N m\(^2\) C\(^{-1}\), what will be the total charge inside the cube? (Given: The permittivity of free space is \(8.85 \times 10^{-12}\) C\(^2\) N\(^{-1}\) m\(^{-2}\)).
- CUET (UG) - 2025
- Physics
- Gauss Law
- An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
- JEE Main - 2024
- Physics
- Gauss Law
- A charge q is placed at the center of one of the surface of a cube. The flux linked with the cube is :-
- JEE Main - 2024
- Physics
- Gauss Law
- There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):

- JEE Main - 2024
- Physics
- Gauss Law
- Match List I with List IIChoose the correct answer from the options given below:
LIST I LIST II A Gauss's Law in Electrostatics I \(\oint \vec{E} \cdot d \vec{l}=-\frac{d \phi_B}{d t}\) B Faraday's Law II \(\oint \vec{B} \cdot d \vec{A}=0\) C Gauss's Law in Magnetism III \(\oint \vec{B} \cdot d \vec{l}=\mu_0 i_c+\mu_0 \in_0 \frac{d \phi_E}{d t}\) D Ampere-Maxwell Law IV \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\epsilon_0}\) - JEE Main - 2023
- Physics
- Gauss Law
Questions Asked in JEE Main exam
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- Ice at \( -5^\circ C \) is heated to become vapor with temperature of \( 110^\circ C \) at atmospheric pressure. The entropy change associated with this process can be obtained from:
- JEE Main - 2025
- Thermodynamics
- Let C be the circle of minimum area enclosing the ellipse E: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \) with eccentricity \( \frac{1}{2} \) and foci \( (\pm 2, 0) \). Let PQR be a variable triangle, whose vertex P is on the circle C and the side QR of length 29 is parallel to the major axis and contains the point of intersection of E with the negative y-axis. Then the maximum area of the triangle PQR is:
- JEE Main - 2025
- Coordinate Geometry
- Let circle $C$ be the image of
$$ x^2 + y^2 - 2x + 4y - 4 = 0 $$
in the line
$$ 2x - 3y + 5 = 0 $$
and $A$ be the point on $C$ such that $OA$ is parallel to the x-axis and $A$ lies on the right-hand side of the centre $O$ of $C$.
If $B(\alpha, \beta)$, with $\beta < 4$, lies on $C$ such that the length of the arc $AB$ is $\frac{1}{6}$ of the perimeter of $C$, then $\beta - \sqrt{3}\alpha$ is equal to: 0.01 mole of an organic compound (X) containing 10% hydrogen, on complete combustion, produced 0.9 g H₂O. Molar mass of (X) is ___________g mol\(^{-1}\).
- JEE Main - 2025
- Organic Chemistry
Concepts Used:
Electric charges and field
What is Electric Charge
It is the property of subatomic particles that experiences a force when put in an electric and magnetic field.
What is Electric Field
It is a property associated with each point in space when charge is present in any form. The magnitude and direction of the electric field are expressed by E, called electric field strength or electric field intensity.
Electric charges are of two types: Positive and Negative. It is commonly carried by charge carriers protons and electrons.
Properties of Electric Charge
Various properties of charge include the following :-
- Additivity of Electric Charge
- Conservation of Electric Charge
- Quantization of Electric Charge
Types of electric charge
Two kinds of electric charges are there :-
Negative Charge - When an object has a negative charge it means that it has more electrons than protons.
Positive Charge - When an object has a positive charge it means that it has more protons than electrons.
When there is an identical number of positive and negative charges, the negative and positive charges would cancel out each other and the object would become neutral.