Question:
A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]
A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]
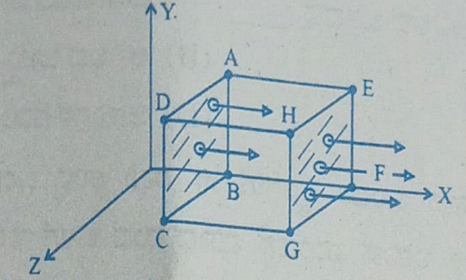
[Take ε0 = 9 × 10-12 Fm-1]
Updated On: Nov 15, 2024
- 1.35 nC
- -1.35 nC
- 0.27 nC
- -0.27 nC
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct answer is (C) : 0.27 nC.
Was this answer helpful?
5
16
Top Questions on Gauss Law
- An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
- JEE Main - 2024
- Physics
- Gauss Law
- A charge q is placed at the center of one of the surface of a cube. The flux linked with the cube is :-
- JEE Main - 2024
- Physics
- Gauss Law
- There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):
- JEE Main - 2024
- Physics
- Gauss Law
A cubical volume is bounded by the surfaces $x=0, x= a , y=0, y= a , z=0, z= a$ The electric field in the region is given by $\vec{E}=E_0 x \hat{ t }$ Where $E_0=4 \times 10^4 NC ^{-1} m ^{-1}$ If $a=2 cm$, the charge contained in the cubical volume is $Q \times 10^{-14} C$ The value of $Q$ is ___ Take \(E_{0}=9\times 10^{-2}C^{2}/Nm^{2}\)
- JEE Main - 2023
- Physics
- Gauss Law
- Match List I with List IIChoose the correct answer from the options given below:
LIST I LIST II A Gauss's Law in Electrostatics I \(\oint \vec{E} \cdot d \vec{l}=-\frac{d \phi_B}{d t}\) B Faraday's Law II \(\oint \vec{B} \cdot d \vec{A}=0\) C Gauss's Law in Magnetism III \(\oint \vec{B} \cdot d \vec{l}=\mu_0 i_c+\mu_0 \in_0 \frac{d \phi_E}{d t}\) D Ampere-Maxwell Law IV \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\epsilon_0}\) - JEE Main - 2023
- Physics
- Gauss Law
View More Questions
Questions Asked in KCET exam
- The speed of sound in an ideal gas at a given temperature T is v. The rms speed of gas molecules at that temperature is vrms. The ratio of the velocities v and vrms for helium and oxygen gases are X and X' respectively. Then \(\frac{X}{X'}\) is equal to
- KCET - 2023
- Thermodynamics
- If \(p(\frac{1}{q}+\frac{1}{r}),q(\frac{1}{r}+\frac{1}{p}),r(\frac{1}{p}+\frac{1}{q})\) are in A.P., then p, q, r
- KCET - 2023
- Arithmetic Progression
- A stretched wire of a material whose Young's modulus Y = 2 × 1011 Nm-2 has Poisson's ratio of 0.25. Its lateral strain εl = 10-3. The elastic energy density of the wire is
- KCET - 2023
- mechanical properties of solids
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Faradays laws of induction
- A 60 W source emits monochromatic light of wavelength 662.5 nm. The number of photons emitted per second is
- KCET - 2023
- Quantum Physics
View More Questions