There are two cubical Gaussian surface carrying charges as shown. Find ratio of fluxes through surface \(C_1\) and \(C_2\):


- \(1:1\)
- \(2:5\)
- \(5:2\)
- \(2:3\)
The Correct Option is B
Solution and Explanation
Top Questions on Gauss Law
- If the net flux through a cube is 1.05 N m\(^2\) C\(^{-1}\), what will be the total charge inside the cube? (Given: The permittivity of free space is \(8.85 \times 10^{-12}\) C\(^2\) N\(^{-1}\) m\(^{-2}\)).
- CUET (UG) - 2025
- Physics
- Gauss Law
- An electric field \( \vec{E} = (2x \hat{i}) \, \text{N C}^{-1} \) exists in space. A cube of side \( 2 \, \text{m} \) is placed in the space as per the figure given below. The electric flux through the cube is __________ \( \text{N m}^2/\text{C} \).
- JEE Main - 2024
- Physics
- Gauss Law
- A charge q is placed at the center of one of the surface of a cube. The flux linked with the cube is :-
- JEE Main - 2024
- Physics
- Gauss Law
- Match List I with List IIChoose the correct answer from the options given below:
LIST I LIST II A Gauss's Law in Electrostatics I \(\oint \vec{E} \cdot d \vec{l}=-\frac{d \phi_B}{d t}\) B Faraday's Law II \(\oint \vec{B} \cdot d \vec{A}=0\) C Gauss's Law in Magnetism III \(\oint \vec{B} \cdot d \vec{l}=\mu_0 i_c+\mu_0 \in_0 \frac{d \phi_E}{d t}\) D Ampere-Maxwell Law IV \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\epsilon_0}\) - JEE Main - 2023
- Physics
- Gauss Law
- A cubical Gaussian surface has side of length a = 10 cm. Electric field lines are parallel to x-axis as shown. The magnitudes of electric fields through surfaces ABCD and EFGH are 6kNC-1 and 9kNC-1 respectively. Then the total charge enclosed by the cube is
[Take ε0 = 9 × 10-12 Fm-1]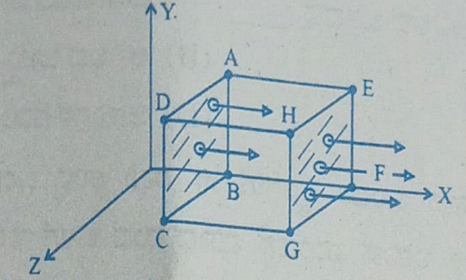
- KCET - 2023
- Physics
- Gauss Law
Questions Asked in JEE Main exam
- Given below are two statements: Statement (I):

Statement (II):
In the light of the above statements, choose the correct answer from the options given below:- JEE Main - 2025
- Isomerism
- Two balls are selected at random one by one without replacement from a bag containing 4 white and 6 black balls. If the probability that the first selected ball is black, given that the second selected ball is also black, is \(\frac{m}{n}\), where gcd(m, n) = 1, then m + n is equal to:
- JEE Main - 2025
- Probability
The integral is given by:
\[ 80 \int_{0}^{\frac{\pi}{4}} \frac{\sin\theta + \cos\theta}{9 + 16 \sin 2\theta} d\theta \]
is equals to?
- JEE Main - 2025
- Integration
- Let \( A(6,8) \), \( B(10\cos\alpha, -10\sin\alpha) \), and \( C(-10\sin\alpha, 10\cos\alpha) \) be the vertices of a triangle. If \( L(a,9) \) and \( G(h,k) \) be its orthocenter and centroid respectively, then \( 5a - 3h + 6k + 100\sin2\alpha \) is equal to _____ .
- JEE Main - 2025
- Coordinate Geometry
- If \[ \sum_{r=1}^{30} r^2 \left( \binom{30}{r} \right)^2 = \alpha \times 2^{29}, \] then \( \alpha \) is equal to _________.
- JEE Main - 2025
- Combinatorics
Concepts Used:
Gauss Law
Gauss law states that the total amount of electric flux passing through any closed surface is directly proportional to the enclosed electric charge.
Gauss Law:
According to the Gauss law, the total flux linked with a closed surface is 1/ε0 times the charge enclosed by the closed surface.

For example, a point charge q is placed inside a cube of edge ‘a’. Now as per Gauss law, the flux through each face of the cube is q/6ε0.
Gauss Law Formula:
As per the Gauss theorem, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. Therefore, if ϕ is total flux and ϵ0 is electric constant, the total electric charge Q enclosed by the surface is;
Q = ϕ ϵ0
The Gauss law formula is expressed by;
ϕ = Q/ϵ0
Where,
Q = total charge within the given surface,
ε0 = the electric constant.