Match List-I with List-II.
List-I List-II (A) Heat capacity of body (I) \( J\,kg^{-1} \) (B) Specific heat capacity of body (II) \( J\,K^{-1} \) (C) Latent heat (III) \( J\,kg^{-1}K^{-1} \) (D) Thermal conductivity (IV) \( J\,m^{-1}K^{-1}s^{-1} \)
Match List-I with List-II.
| List-I | List-II |
| (A) Heat capacity of body | (I) \( J\,kg^{-1} \) |
| (B) Specific heat capacity of body | (II) \( J\,K^{-1} \) |
| (C) Latent heat | (III) \( J\,kg^{-1}K^{-1} \) |
| (D) Thermal conductivity | (IV) \( J\,m^{-1}K^{-1}s^{-1} \) |
Show Hint
- (A)-(III), (B)-(I), (C)-(II), (D)-(IV)
- (A)-(I), (B)-(III), (C)-(II), (D)-(IV)
- (A)-(III), (B)-(IV), (C)-(I), (D)-(II)
(A)-(II), (B)-(III), (C)-(I), (D)-(IV)
The Correct Option is D
Solution and Explanation
We are asked to match physical quantities with their SI units.
Step-by-Step Solution:
(A) Heat capacity of a body:
\[ \text{Unit: } \frac{\text{Joule}}{\text{Kelvin}} = \text{J K}^{-1} \] Hence, (A) → (II)
(B) Specific heat capacity of a body:
\[ \text{Unit: } \frac{\text{Joule}}{\text{kilogram} \cdot \text{Kelvin}} = \text{J kg}^{-1} \text{K}^{-1} \] Hence, (B) → (III)
(C) Latent heat:
\[ \text{Unit: } \frac{\text{Joule}}{\text{kilogram}} = \text{J kg}^{-1} \] Hence, (C) → (I)
(D) Thermal conductivity:
\[ \text{Unit: } \frac{\text{Joule}}{\text{metre} \cdot \text{second} \cdot \text{Kelvin}} = \text{J m}^{-1} \text{K}^{-1} \text{s}^{-1} \] Hence, (D) → (IV)
Final Matching:
| List-I | List-II |
|---|---|
| (A) Heat capacity of body | (II) J K-1 |
| (B) Specific heat capacity of body | (III) J kg-1 K-1 |
| (C) Latent heat | (I) J kg-1 |
| (D) Thermal conductivity | (IV) J m-1 K-1 s-1 |
Final Answer:
\[ \boxed{(A) \to (II), \quad (B) \to (III), \quad (C) \to (I), \quad (D) \to (IV)} \]
Top Questions on specific heat capacity
- Product of uncertainty in position (\(\Delta x\)) and uncertainty in velocity (\(\Delta v\)) has unit:
- KEAM - 2025
- Physics
- specific heat capacity
- If \( \frac{C_p}{C_v} \) is unity for a process, \( PV^{\gamma} = \text{constant} \), then the process is:
- KEAM - 2025
- Physics
- specific heat capacity
- Specific heat capacity of diatomic gas at constant volume:
- KEAM - 2025
- Physics
- specific heat capacity
In the given cycle ABCDA, the heat required for an ideal monoatomic gas will be:

- BITSAT - 2024
- Physics
- specific heat capacity
- The circuit shown in the figure contains an inductor L, a capacitor \(C_0\), a resistor\( R_0\) and an ideal battery. The circuit also contains two keys \(K_1\) and \(K_2\). Initially, both the keys are open and there is no charge on the capacitor. At an instant, key \(K_1\) is closed and immediately after this the current in \(R_0\) is found to be \(I_1\). After a long time, the current attains a steady state value \(I_2\). Thereafter,\( K_2\) is closed and simultaneously \(K_1\) is opened and the voltage across \(C_0\) oscillates with amplitude \(C_0\) and angular frequency \(\omega_0\).
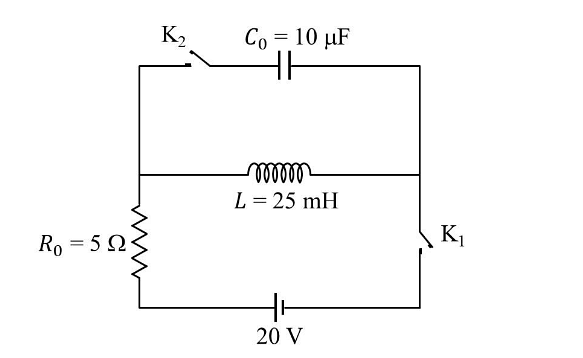
Match the quantities mentioned in List-I with their values in List-II and choose the correct option.List-I List-II P The value of \(I1\) in Ampere is I \(0\) Q The value of I2 in Ampere is II \(2\) R The value of \(\omega_0\) in kilo-radians/s is III \(4\) S The value of \(V_0\) in Volt is IV \(20\) 200 - JEE Advanced - 2024
- Physics
- specific heat capacity
Questions Asked in JEE Main exam
- The sum of all possible values of \( n \in \mathbb{N} \), so that the coefficients of \(x, x^2\) and \(x^3\) in the expansion of \((1+x^2)^2(1+x)^n\) are in arithmetic progression is :
- JEE Main - 2026
- Integration
- In a microscope of tube length $10\,\text{cm}$ two convex lenses are arranged with focal lengths $2\,\text{cm}$ and $5\,\text{cm}$. Total magnification obtained with this system for normal adjustment is $(5)^k$. The value of $k$ is ___.
- JEE Main - 2026
- Optical Instruments
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
- Let \( ABC \) be an equilateral triangle with orthocenter at the origin and the side \( BC \) lying on the line \( x+2\sqrt{2}\,y=4 \). If the coordinates of the vertex \( A \) are \( (\alpha,\beta) \), then the greatest integer less than or equal to \( |\alpha+\sqrt{2}\beta| \) is:
- JEE Main - 2026
- Coordinate Geometry
- Three charges $+2q$, $+3q$ and $-4q$ are situated at $(0,-3a)$, $(2a,0)$ and $(-2a,0)$ respectively in the $x$-$y$ plane. The resultant dipole moment about origin is ___.
- JEE Main - 2026
- Electromagnetic waves