Expression for an electric field is given by $\overrightarrow{ E }=4000 x^2 i \frac{ V }{ m }$ The electric flux through the cube of side $20 cm$ when placed in electric field (as shown in the figure) is ___$V cm$

Expression for an electric field is given by $\overrightarrow{ E }=4000 x^2 i \frac{ V }{ m }$ The electric flux through the cube of side $20 cm$ when placed in electric field (as shown in the figure) is ___$V cm$
Show Hint
Correct Answer: 640
Approach Solution - 1
The correct answer is 640
Flux \(=\vec{E}⋅\vec{A} \)
\(=4000(0⋅2)^2\frac{V}{m}⋅(0⋅2)^2m^2 \)
=4000×16×10−4Vm
=640 Vcm
Approach Solution -2
\[ \Phi_E = \vec{E} \cdot \vec{A} \]
where \( \vec{E} \) is the electric field and \( \vec{A} \) is the area vector. The area of one face of the cube is:\[ A = (0.2 \, \text{m})^2 = 0.04 \, \text{m}^2 \]
Since the electric field is along the \( x \)-axis and the area vector is normal to the face of the cube, we have:\[ \Phi_E = E \times A = 4000 \times (0.2)^2 = 4000 \times 0.04 = 640 \, \text{Vcm} \]
Thus, the electric flux is 640 Vcm.Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
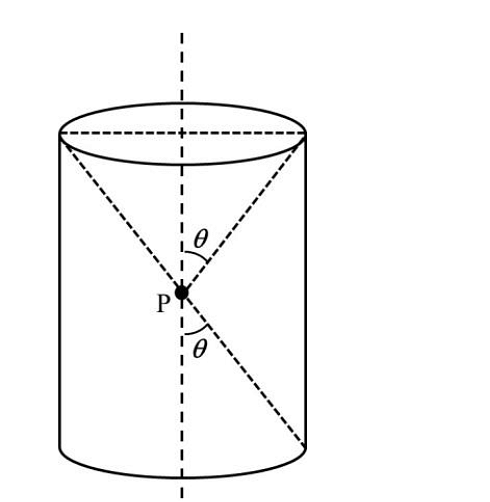
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in JEE Main exam
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- The area of the region enclosed by the curves \( y = x^2 - 4x + 4 \) and \( y^2 = 16 - 8x \) is:
- JEE Main - 2025
- Area between Two Curves
- 2.8 \( \times 10^{-3} \) mol of \( \text{CO}_2 \) is left after removing \( 10^{21} \) molecules from its ‘\( x \)’ mg sample. The mass of \( \text{CO}_2 \) taken initially is: Given: \( N_A = 6.02 \times 10^{23} \, \text{mol}^{-1} \)
- JEE Main - 2025
- Mole concept and Molar Masses
- A conducting bar moves on two conducting rails as shown in the figure. A constant magnetic field \( B \) exists into the page. The bar starts to move from the vertex at time \( t = 0 \) with a constant velocity. If the induced EMF is \( E \propto t^n \), then the value of \( n \) is ________________________.

- JEE Main - 2025
- Electromagnetic induction

In the first configuration (1) as shown in the figure, four identical charges \( q_0 \) are kept at the corners A, B, C and D of square of side length \( a \). In the second configuration (2), the same charges are shifted to mid points C, E, H, and F of the square. If \( K = \frac{1}{4\pi \epsilon_0} \), the difference between the potential energies of configuration (2) and (1) is given by:
- JEE Main - 2025
- Electromagnetic Field (EMF)
Concepts Used:
Electric charges and field
What is Electric Charge
It is the property of subatomic particles that experiences a force when put in an electric and magnetic field.
What is Electric Field
It is a property associated with each point in space when charge is present in any form. The magnitude and direction of the electric field are expressed by E, called electric field strength or electric field intensity.
Electric charges are of two types: Positive and Negative. It is commonly carried by charge carriers protons and electrons.
Properties of Electric Charge
Various properties of charge include the following :-
- Additivity of Electric Charge
- Conservation of Electric Charge
- Quantization of Electric Charge
Types of electric charge
Two kinds of electric charges are there :-
Negative Charge - When an object has a negative charge it means that it has more electrons than protons.
Positive Charge - When an object has a positive charge it means that it has more protons than electrons.
When there is an identical number of positive and negative charges, the negative and positive charges would cancel out each other and the object would become neutral.