Question:
The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
Show Hint
In transverse waves, the particle velocity is perpendicular to the direction of wave propagation, except at the mean position where the velocities align momentarily.
Updated On: Apr 16, 2025
- \( \pi \, \text{radian} \)
- \( \frac{\pi}{2} \, \text{radian} \)
- Zero radian
- \( \frac{\pi}{4} \, \text{radian} \)
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
In a transverse wave, the particle velocity is always perpendicular to the displacement of the particle, and the wave velocity is along the direction of propagation of the wave. - The particle velocity is the velocity at which each particle of the medium moves as the wave passes. This velocity is tangential to the particle's motion. - The wave velocity, on the other hand, is the velocity at which the wave moves through the medium, propagating from one point to another. At any point except when the particle passes through the mean position (where the particle is momentarily stationary), the angle between the particle velocity and the wave velocity is \( \frac{\pi}{2} \, \text{radians} \). This is because the particle moves perpendicular to the direction of wave propagation. Thus, the angle between the particle velocity and wave velocity is \( \frac{\pi}{2} \, \text{radian} \).
Was this answer helpful?
0
0
Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
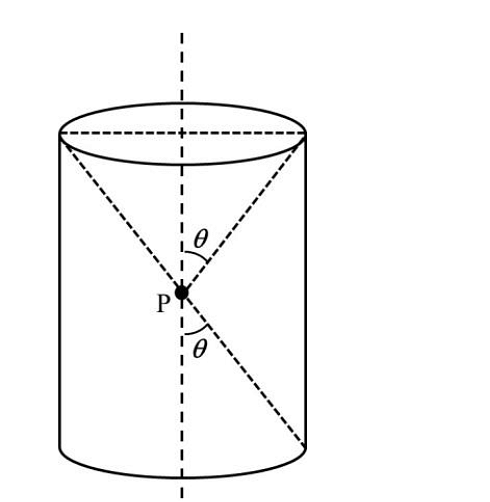
- JEE Advanced - 2024
- Physics
- Electric Flux
- Five charges +q, +5q, –2q, +3q and –4q are situated as shown in the figure. The electric flux due to this configuration through the surface S is

- JEE Main - 2024
- Physics
- Electric Flux
View More Questions
Questions Asked in KCET exam
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- Ethyl alcohol is heated with concentrated sulphuric acid at 413 K (140°C). The major product formed is
- KCET - 2025
- Organic Chemistry
- A body of mass 0.25 kg travels along a straight line from \( x = 0 \) to \( x = 2 \, \text{m} \) with a speed \( v = k x^2 \) where \( k = 2 \, \text{m}^{-1} \). The work done by the net force during this displacement is
- KCET - 2025
- Elastic and inelastic collisions
- A square loop of side 2 m lies in the Y-Z plane in a region having a magnetic field \(\mathbf{B} = (5 \hat{i} - 3 \hat{j} - 4 \hat{k}) \, \text{T}\). The magnitude of magnetic flux through the square loop is
- KCET - 2025
- Magnetic Field
- A random experiment has five outcomes \(w_1, w_2, w_3, w_4, w_5\). The probabilities of the occurrence of the outcomes \(w_1, w_2, w_4, w_5\) are respectively \( \frac{1}{6}, a, b, \frac{1}{12} \) such that \(12a + 12b - 1 = 0\). Then the probabilities of occurrence of the outcome \(w_3\) is:
- KCET - 2025
- Probability
View More Questions