An electric field \( \vec{E} \) is given by:
\[
\vec{E} =
\begin{cases}
+100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\
-100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0
\end{cases}
\]
A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate:
(a) the net outward flux through the cylinder, and
(b) the net charge inside the cylinder.
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.
Show Hint
Solution and Explanation
(a) Net outward flux = \( 0 \, \text{Nm}^2/\text{C} \)
(b) Net charge inside the cylinder = \( 0 \, \text{C} \)
Top Questions on Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
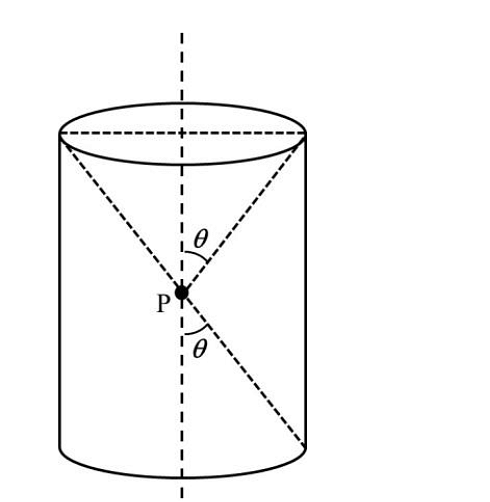
- JEE Advanced - 2024
- Physics
- Electric Flux
- Five charges +q, +5q, –2q, +3q and –4q are situated as shown in the figure. The electric flux due to this configuration through the surface S is

- JEE Main - 2024
- Physics
- Electric Flux
Questions Asked in CBSE CLASS XII exam
- State Kirchhoff’s laws. Apply these laws to find the values of current flowing in the three branches of the given circuit.

- CBSE CLASS XII - 2025
- Kirchhoff's Laws
On the basis of the following hypothetical data, calculate the percentage change in Real Gross Domestic Product (GDP) in the year 2022 – 23, using 2020 – 21 as the base year.
Year Nominal GDP Nominal GDP (Adjusted to Base Year Price) 2020–21 3,000 5,000 2022–23 4,000 6,000 - CBSE CLASS XII - 2025
- National Income Accounting
- A double convex lens of glass has both faces of the same radius of curvature 17 cm. Find its focal length if it is immersed in water. The refractive indices of glass and water are 1.5 and 1.33 respectively.
- The matrix $A = \begin{bmatrix} \sqrt{5} & 0 & 0 \\ 0 & \sqrt{2} & 0 \\ 0 & 0 & \sqrt{5} \end{bmatrix}$ is an:
- Read the following statements carefully:
Statement 1: The Food Corporation of India maintains buffer stocks of wheat and rice as a measure to improve market mechanism.
Statement 2: Minimum Support Price (MSP) is imposed by the government to safeguard the interest of farmers.
In the light of the given statements, choose the correct option from the following:- CBSE CLASS XII - 2025
- Agriculture