A charge is kept at the central point \( P \) of a cylindrical region. The two edges subtend a half-angle \(\theta\) at \( P \), as shown in the figure. When \(\theta = 30^\circ\), then the electric flux through the curved surface of the cylinder is \(\Phi\). If \(\theta = 60^\circ\), then the electric flux through the curved surface becomes \(\frac{\Phi}{\sqrt{n}}\), where the value of \(n\) is \_\_\_\_.
\includegraphics[width=0.3\linewidth]{ph8.png}
Show Hint
Solution and Explanation
Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
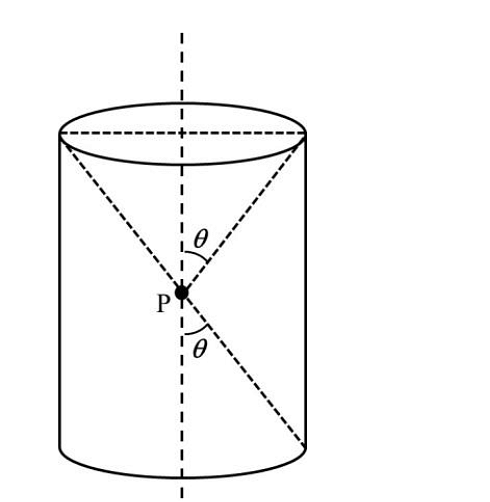
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in JEE Advanced exam
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):

- JEE Advanced - 2025
- Waves and Oscillations
- Consider the vectors $$ \vec{x} = \hat{i} + 2\hat{j} + 3\hat{k},\quad \vec{y} = 2\hat{i} + 3\hat{j} + \hat{k},\quad \vec{z} = 3\hat{i} + \hat{j} + 2\hat{k}. $$ For two distinct positive real numbers $ \alpha $ and $ \beta $, define $$ \vec{X} = \alpha \vec{x} + \beta \vec{y} - \vec{z},\quad \vec{Y} = \alpha \vec{y} + \beta \vec{z} - \vec{x},\quad \vec{Z} = \alpha \vec{z} + \beta \vec{x} - \vec{y}. $$ If the vectors $ \vec{X}, \vec{Y}, \vec{Z} $ lie in a plane, then the value of $ \alpha + \beta - 3 $ is ________.