Question:
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)? 
Show Hint
According to Gauss’s law, the electric flux through a surface depends on the charge enclosed by that surface. Inside a conductor, there is no enclosed charge, so the electric flux is zero.
Updated On: Apr 18, 2025
- \( \frac{Q}{4\pi \epsilon_0 R^2} \)
- \( \frac{Q}{\epsilon_0} \)
- \( \frac{Q}{4\pi \epsilon_0 R_4^2} \)
- Zero
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
To find the electric flux at any point inside the metallic sphere of radius \( R \), we need to apply Gauss's Law, which states: \[ \Phi = \frac{Q_{\text{enc}}}{\epsilon_0} \] where \( \Phi \) is the electric flux, \( Q_{\text{enc}} \) is the charge enclosed by the Gaussian surface, and \( \epsilon_0 \) is the permittivity of free space. For a point inside the metallic sphere of radius \( R \), the Gaussian surface inside the sphere does not enclose any charge. This is because the metallic sphere of radius \( R \) has no charge inside it; the charge \( q \) is distributed on the surface of the sphere. Thus, the electric flux at any point inside the metallic sphere of radius \( R \) due to the charge \( Q \) on the sphere of radius \( R_4 \) is zero, because the Gaussian surface inside the sphere does not enclose any charge. Therefore, the electric flux is: \[ \Phi = 0 \] Thus, the correct answer is zero.
Was this answer helpful?
0
2
Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
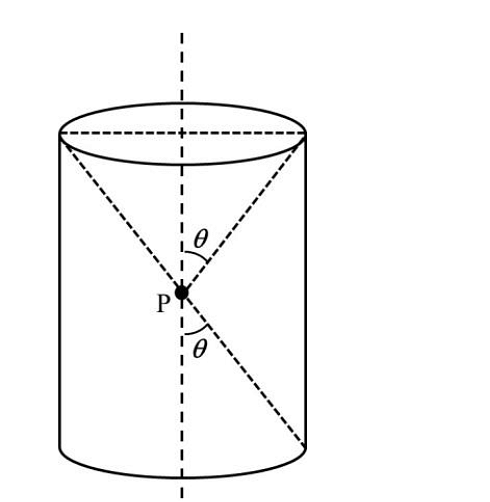
- JEE Advanced - 2024
- Physics
- Electric Flux
- Five charges +q, +5q, –2q, +3q and –4q are situated as shown in the figure. The electric flux due to this configuration through the surface S is

- JEE Main - 2024
- Physics
- Electric Flux
View More Questions
Questions Asked in KCET exam
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- Ethyl alcohol is heated with concentrated sulphuric acid at 413 K (140°C). The major product formed is
- KCET - 2025
- Organic Chemistry
- A body of mass 0.25 kg travels along a straight line from \( x = 0 \) to \( x = 2 \, \text{m} \) with a speed \( v = k x^2 \) where \( k = 2 \, \text{m}^{-1} \). The work done by the net force during this displacement is
- KCET - 2025
- Elastic and inelastic collisions
- A square loop of side 2 m lies in the Y-Z plane in a region having a magnetic field \(\mathbf{B} = (5 \hat{i} - 3 \hat{j} - 4 \hat{k}) \, \text{T}\). The magnitude of magnetic flux through the square loop is
- KCET - 2025
- Magnetic Field
- A random experiment has five outcomes \(w_1, w_2, w_3, w_4, w_5\). The probabilities of the occurrence of the outcomes \(w_1, w_2, w_4, w_5\) are respectively \( \frac{1}{6}, a, b, \frac{1}{12} \) such that \(12a + 12b - 1 = 0\). Then the probabilities of occurrence of the outcome \(w_3\) is:
- KCET - 2025
- Probability
View More Questions