Question:
circles (concyclic, 3 pts given and do they form equilateral, right angled triangle)
circles (concyclic, 3 pts given and do they form equilateral, right angled triangle)
Updated On: Jun 23, 2024
Hide Solution
Verified By Collegedunia
Solution and Explanation
To determine if three points are concyclic (lie on the same circle), we can use the concept of the circumcenter. The circumcenter is the center of the circle that passes through all three points.
If three points form an equilateral triangle, they are always concyclic. An equilateral triangle has all three sides of equal length and all three angles equal to 60 degrees.
If three points form a right-angled triangle, they may or may not be concyclic. A right-angled triangle has one angle measuring 90 degrees. However, for the three points to be concyclic, the right angle must be subtended by the diameter of the circle.
To check if the given three points form an equilateral triangle or a right-angled triangle, you need to provide the coordinates or describe the points in more detail.
If three points form an equilateral triangle, they are always concyclic. An equilateral triangle has all three sides of equal length and all three angles equal to 60 degrees.
If three points form a right-angled triangle, they may or may not be concyclic. A right-angled triangle has one angle measuring 90 degrees. However, for the three points to be concyclic, the right angle must be subtended by the diameter of the circle.
To check if the given three points form an equilateral triangle or a right-angled triangle, you need to provide the coordinates or describe the points in more detail.
Was this answer helpful?
2
1
Top Questions on Three Dimensional Geometry
- If the foot is perpendicular from (1, 2, 3) to the line \(\frac{x+1}{2} = \frac{y-2}{5} = \frac{z-1}{1}\) is \(( a, \beta, \gamma)\), then find \(a + \beta + \gamma\)
- JEE Main - 2024
- Mathematics
- Three Dimensional Geometry
- Let R3 denote the three-dimensional space. Take two points P = (1, 2, 3) and Q = (4, 2 ,7). Let
dist(X, Y) denote the distance between two points X and Y in R3. Let
\(S=\left\{X\in\R^3:(dist(X,P)^2)-(dist(X,Q))^2=50\right\}\ and\)
\(T=\left\{Y\in \R^3:(dist(Y,Q))^2-(dist(Y,P))^2=50\right\}\)
Then which of the following statements is (are) TRUE ?- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- A straight line drawn from the point P(1,3, 2), parallel to the line \(\frac{x-2}{1}=\frac{y-4}{2}=\frac{z-6}{1}\), intersects the plane L1 : x - y + 3z = 6 at the point Q. Another straight line which passes through Q and is perpendicular to the plane L1 intersects the plane L2 : 2x - y + z = -4 at the point R. Then which of the following statements is (are) TRUE ?
- JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- Let y ∈ R be such that the lines \(L_1:\frac{x+11}{1}=\frac{y+21}{2}=\frac{z+29}{3}\) and \(L_2:\frac{x+16}{3}=\frac{y+11}{2}=\frac{z+4}{\gamma}\) intersect. Let R1 be the point of intersection of L1 and L2. Let O = (0, 0 ,0), and \(\hat{n}\) denote a unit normal vector to the plane containing both the lines L1 and L2.
Match each entry in List-I to the correct entry in List-II.The correct option isList - I List - II (P) γ equals (1) \(-\hat{i}-\hat{j}+\hat{k}\) (Q) A possible choice for \(\hat{n}\) is (2) \(\sqrt{\frac{3}{2}}\) (R) \(\overrightarrow{OR_1}\) equals (3) 1 (S) A possible value of \(\overrightarrow{OR_1}.\hat{n}\) is (4) \(\frac{1}{\sqrt6}\hat{i}-\frac{2}{\sqrt6}\hat{j}+\frac{1}{\sqrt6}\hat{k}\) (5) \(\sqrt{\frac{2}{3}}\) - JEE Advanced - 2024
- Mathematics
- Three Dimensional Geometry
- The length of the perpendicular drawn from the point \((1, 2, 3)\) to the line \((X - 6)/3 = (y - 7)/2 = (Z - 7)/-2\) is:
- MHT CET - 2024
- Mathematics
- Three Dimensional Geometry
View More Questions
Questions Asked in BITSAT exam
- Let \( ABC \) be a triangle and \( \vec{a}, \vec{b}, \vec{c} \) be the position vectors of \( A, B, C \) respectively. Let \( D \) divide \( BC \) in the ratio \( 3:1 \) internally and \( E \) divide \( AD \) in the ratio \( 4:1 \) internally. Let \( BE \) meet \( AC \) in \( F \). If \( E \) divides \( BF \) in the ratio \( 3:2 \) internally then the position vector of \( F \) is:
- BITSAT - 2024
- Vectors
- Let \( \mathbf{a} = \hat{i} - \hat{k}, \mathbf{b} = x\hat{i} + \hat{j} + (1 - x)\hat{k}, \mathbf{c} = y\hat{i} + x\hat{j} + (1 + x - y)\hat{k} \). Then, \( [\mathbf{a} \, \mathbf{b} \, \mathbf{c}] \) depends on:}
- BITSAT - 2024
- Vectors
- Let the foot of perpendicular from a point \( P(1,2,-1) \) to the straight line \( L : \frac{x}{1} = \frac{y}{0} = \frac{z}{-1} \) be \( N \). Let a line be drawn from \( P \) parallel to the plane \( x + y + 2z = 0 \) which meets \( L \) at point \( Q \). If \( \alpha \) is the acute angle between the lines \( PN \) and \( PQ \), then \( \cos \alpha \) is equal to:
- The magnitude of projection of the line joining \( (3,4,5) \) and \( (4,6,3) \) on the line joining \( (-1,2,4) \) and \( (1,0,5) \) is:
- BITSAT - 2024
- Vectors
- The angle between the lines whose direction cosines are given by the equations \( 3l + m + 5n = 0 \) and \( 6m - 2n + 5l = 0 \) is:
- BITSAT - 2024
- Vectors
View More Questions
Concepts Used:
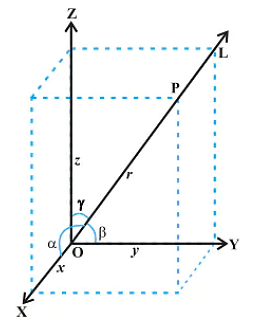
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.
