Two metallic rings $A$ and $B$, identical in shape and size but having different resistivities $\rho_A \, and \, \rho_B$, are kept on top of two
identical solenoids as shown in the figure. When current $I$ is switched on in both the solenoids in identical manner, the rings $A$ and $B$ jump to heights $h_A \, and \, h_B$, respectively, with $h_A > h_B$. The possible relation(s) between their resistivities and their masses $m_A$ and $m_B$ is (are)
- $\rho_A > \rho_B $ and $ m_A = m_B $
- $\rho_A
- $\rho_A >\, \rho_B $ and $ m_A >\, m_B $
- $\rho_A < \rho_B$ and $ m_A < m_B $
The Correct Option is D
Solution and Explanation
be same. But currents will be different. Given $h_A > h_B$.
Hence, $v_A > v_B \, as \bigg( h = \frac{v^2}{2g}\bigg).$
If $\rho_A > \rho_B$, then, $I_A < I_B$. In this case given condition can be
fulfilled if $m_A < m_B$.
If $\rho_A < \rho_B$, then $I_A > I_B$. In this case given condition can be
fulfilled if $m_A \le m_B$
Top Questions on Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )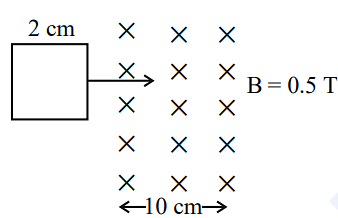
- KCET - 2023
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
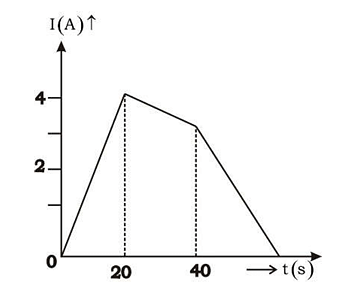
- KCET - 2021
- Physics
- Faradays laws of induction
Questions Asked in JEE Advanced exam
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):

- JEE Advanced - 2025
- Waves and Oscillations
- Consider the vectors $$ \vec{x} = \hat{i} + 2\hat{j} + 3\hat{k},\quad \vec{y} = 2\hat{i} + 3\hat{j} + \hat{k},\quad \vec{z} = 3\hat{i} + \hat{j} + 2\hat{k}. $$ For two distinct positive real numbers $ \alpha $ and $ \beta $, define $$ \vec{X} = \alpha \vec{x} + \beta \vec{y} - \vec{z},\quad \vec{Y} = \alpha \vec{y} + \beta \vec{z} - \vec{x},\quad \vec{Z} = \alpha \vec{z} + \beta \vec{x} - \vec{y}. $$ If the vectors $ \vec{X}, \vec{Y}, \vec{Z} $ lie in a plane, then the value of $ \alpha + \beta - 3 $ is ________.
- If $$ \alpha = \int_{\frac{1}{2}}^{2} \frac{\tan^{-1} x}{2x^2 - 3x + 2} \, dx, $$ then the value of $ \sqrt{7} \tan \left( \frac{2\alpha \sqrt{7}}{\pi} \right) $ is.
(Here, the inverse trigonometric function $ \tan^{-1} x $ assumes values in $ \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) $.)- JEE Advanced - 2025
- Integral Calculus
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Concepts Used:
Faradays Laws of Induction
There are two laws, given by Faraday which explain the phenomena of electromagnetic induction:
Faraday's First Law:
Whenever a conductor is placed in a varying magnetic field, an emf is induced. If the conductor circuit is closed, a current is induced, known as the induced current.
Faraday's Second Law:
The Emf induced inside a coil is equal to the rate of change of associated magnetic flux.
This law can be mathematically written as:
∈\(-N {\triangle \phi \over \triangle t}\)
