In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- 5 mH
- 1 mH
- 2.5 mH
- 4 mH
The Correct Option is A
Approach Solution - 1
To determine the self-inductance of the coil, we can use the following formula that relates the induced electromotive force (emf) in a coil to its self-inductance and the rate of change of current through it:
\(E = -L \frac{\Delta I}{\Delta t}\)
Where:
- \(E\) is the induced emf (0.1 V in this case).
- \(L\) is the self-inductance of the coil.
- \(\Delta I\) is the change in current (-2 A to +2 A, so \(\Delta I = 2 - (-2) = 4 \, \text{A}\)).
- \(\Delta t\) is the time interval over which the current changes (0.2 s).
Rearranging the formula to solve for \(L\), we have:
\(L = -\frac{E \cdot \Delta t}{\Delta I}\)
Substitute the given values into this formula:
\(L = -\frac{0.1 \, \text{V} \cdot 0.2 \, \text{s}}{4 \, \text{A}}\)
\(L = -\frac{0.02}{4}\)
\(L = -0.005 \, \text{H}\)
Since inductance is conventionally given as a positive value, we take the absolute value:
\(L = 0.005 \, \text{H} = 5 \, \text{mH}\)
Thus, the self-inductance of the coil is 5 mH.
Let's analyze the options:
- 5 mH: Correct, matches calculated value.
- 1 mH: Incorrect.
- 2.5 mH: Incorrect.
- 4 mH: Incorrect.
Therefore, the correct answer is 5 mH.
Approach Solution -2
The induced emf in a coil is given by:\[(\text{Emf})_{\text{induced}} = -L \frac{di}{dt}\]
In terms of magnitude:
\[|\text{Emf}_{\text{induced}}| = \left| L \frac{di}{dt} \right|\]
Given:
\[|\text{Emf}_{\text{induced}}| = 0.1 \, \text{V}\]
\[\frac{di}{dt} = \frac{2 - (-2)}{0.2} = \frac{4}{0.2} = 20 \, \text{A/s}\]
Now, solve for \( L \):
\[0.1 = L \times 20\]
\[L = \frac{0.1}{20} = 0.005 \, \text{H} = 5 \, \text{mH}\]
Top Questions on Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )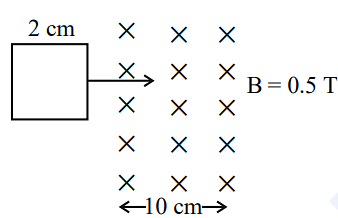
- KCET - 2023
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
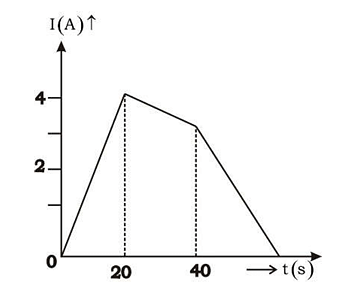
- KCET - 2021
- Physics
- Faradays laws of induction
- A wheel with $20$ metallic spokes each $1\, m$ long is rotated with a speed of $120\, rpm$ in a plane perpendicular to a magnetic field of $0.4\, G$. The induced emf between the axle and rim of the wheel will be, $(1 G = 10^{-4}\, T)$
- NEET (UG) - 2020
- Physics
- Faradays laws of induction
Questions Asked in JEE Main exam
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- Ice at \( -5^\circ C \) is heated to become vapor with temperature of \( 110^\circ C \) at atmospheric pressure. The entropy change associated with this process can be obtained from:
- JEE Main - 2025
- Thermodynamics
- Let C be the circle of minimum area enclosing the ellipse E: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \) with eccentricity \( \frac{1}{2} \) and foci \( (\pm 2, 0) \). Let PQR be a variable triangle, whose vertex P is on the circle C and the side QR of length 29 is parallel to the major axis and contains the point of intersection of E with the negative y-axis. Then the maximum area of the triangle PQR is:
- JEE Main - 2025
- Coordinate Geometry
- Let circle $C$ be the image of
$$ x^2 + y^2 - 2x + 4y - 4 = 0 $$
in the line
$$ 2x - 3y + 5 = 0 $$
and $A$ be the point on $C$ such that $OA$ is parallel to the x-axis and $A$ lies on the right-hand side of the centre $O$ of $C$.
If $B(\alpha, \beta)$, with $\beta < 4$, lies on $C$ such that the length of the arc $AB$ is $\frac{1}{6}$ of the perimeter of $C$, then $\beta - \sqrt{3}\alpha$ is equal to: 0.01 mole of an organic compound (X) containing 10% hydrogen, on complete combustion, produced 0.9 g H₂O. Molar mass of (X) is ___________g mol\(^{-1}\).
- JEE Main - 2025
- Organic Chemistry