Question:
A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )
A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )
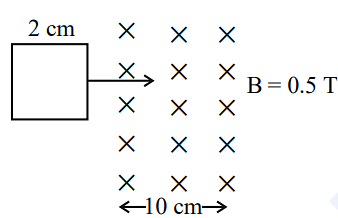
( Take clockwise direction positive )
Updated On: Jul 23, 2024
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct answer is (C) : 
.
.Was this answer helpful?
2
12
Top Questions on Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
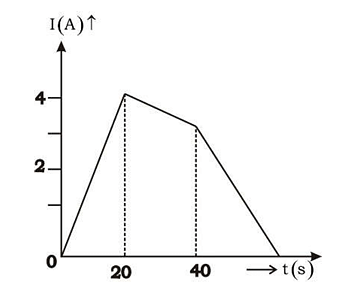
- KCET - 2021
- Physics
- Faradays laws of induction
- A wheel with $20$ metallic spokes each $1\, m$ long is rotated with a speed of $120\, rpm$ in a plane perpendicular to a magnetic field of $0.4\, G$. The induced emf between the axle and rim of the wheel will be, $(1 G = 10^{-4}\, T)$
- NEET (UG) - 2020
- Physics
- Faradays laws of induction
View More Questions
Questions Asked in KCET exam
- The speed of sound in an ideal gas at a given temperature T is v. The rms speed of gas molecules at that temperature is vrms. The ratio of the velocities v and vrms for helium and oxygen gases are X and X' respectively. Then \(\frac{X}{X'}\) is equal to
- KCET - 2023
- Thermodynamics
- If \(p(\frac{1}{q}+\frac{1}{r}),q(\frac{1}{r}+\frac{1}{p}),r(\frac{1}{p}+\frac{1}{q})\) are in A.P., then p, q, r
- KCET - 2023
- Arithmetic Progression
- A stretched wire of a material whose Young's modulus Y = 2 × 1011 Nm-2 has Poisson's ratio of 0.25. Its lateral strain εl = 10-3. The elastic energy density of the wire is
- KCET - 2023
- mechanical properties of solids
- A 60 W source emits monochromatic light of wavelength 662.5 nm. The number of photons emitted per second is
- KCET - 2023
- Quantum Physics
- A weak acid with pKa 5.9 and weak base with pKb 5.8 are mixed in equal proportions. pH of the resulting solution is
- KCET - 2023
- Acids and Bases
View More Questions