The orthocenter of the triangle whose sides are given by x + y + 10 = 0, x - y - 2 = 0 and 2x + y - 7 = 0 is
The orthocenter of the triangle whose sides are given by x + y + 10 = 0, x - y - 2 = 0 and 2x + y - 7 = 0 is
(-4, -3)
(-4, -6)
(4,6)
(3,6)
The Correct Option is B
Solution and Explanation
To find the vertex of the triangle formed by the lines \(x + y + 10 = 0\), \(x - y - 2 = 0\), and \(2x + y - 7 = 0\)
1. Finding the First Vertex:
Solve for the intersection of \(x + y + 10 = 0\) and \(x - y - 2 = 0\):
\( x + y = -10 \quad (1) \)
\( x - y = 2 \quad (2) \)
Add the equations:
\( (x + y) + (x - y) = -10 + 2 \)
\( 2x = -8 \implies x = -4 \)
Substitute \(x = -4\) into (2):
\( -4 - y = 2 \implies y = -6 \)
Thus, the intersection is \((-4, -6)\).
2. Verifying Other Vertices:
Solve for the intersection of \(x - y - 2 = 0\) and \(2x + y - 7 = 0\):
\( x - y = 2 \quad (1) \)
\( 2x + y = 7 \quad (2) \)
Add the equations:
\( (x - y) + (2x + y) = 2 + 7 \)
\( 3x = 9 \implies x = 3 \)
Substitute \(x = 3\) into (1):
\( 3 - y = 2 \implies y = 1 \)
So, the intersection is \((3, 1)\).
3. Third Vertex:
Solve for the intersection of \(x + y + 10 = 0\) and \(2x + y - 7 = 0\):
\( x + y = -10 \quad (1) \)
\( 2x + y = 7 \quad (2) \)
Subtract (1) from (2):
\( (2x + y) - (x + y) = 7 - (-10) \)
\( x = 17 \)
Substitute \(x = 17\) into (1):
\( 17 + y = -10 \implies y = -27 \)
So, the intersection is \((17, -27)\).
\( 2(-4) - 3(-6) + k = -8 + 18 + k = 10 + k = 0 \implies k = -10 \)
However, using \(2x - 3y - 10 = 0\) makes all three lines concurrent at \((-4, -6)\), which does not form a triangle.
Thus, the original line \(2x + y - 7 = 0\) is likely correct, as it yields \((-4, -6)\) as a vertex.
Final Answer:
The vertex is \((-4, -6)\).
Top Questions on Three Dimensional Geometry
- If A(2,1,-1), B(6,-3,2), C(-3,12,4) are the vertices of a triangle ABC and the equation of the plane containing the triangle ABC is $53x+by+cz+d=0$, then $\frac{d}{b+c}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If $(\alpha, \beta, \gamma)$ is the foot of the perpendicular drawn from a point $(-1,2,-1)$ to the line joining the points $(2,-1,1)$ and $(1,1,-2)$, then $\alpha+\beta+\gamma=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If m:n is the ratio in which the point $\left(\frac{8}{5}, \frac{1}{5}, \frac{8}{5}\right)$ divides the line segment joining the points (2,p,2) and (p,-2,p) where p is an integer then $\frac{3m+n}{3n}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- Let $\pi_1$ be the plane determined by the vectors $\hat{i}+\hat{j}, \hat{i}+\hat{k}$ and $\pi_2$ be the plane determined by the vectors $\hat{j}-\hat{k}, \hat{k}-\hat{i}$. Let $\vec{a}$ be a non-zero vector parallel to the line of intersection of the planes $\pi_1$ and $\pi_2$. If $\vec{b} = \hat{i}+\hat{j}-\hat{k}$ then the angle between the vectors $\vec{a}$ and $\vec{b}$ is
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
Show that the following lines intersect. Also, find their point of intersection:
Line 1: \[ \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} \]
Line 2: \[ \frac{x - 4}{5} = \frac{y - 1}{2} = z \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
Questions Asked in TS EAMCET exam
- Identify the correct matching pair to Calvin cycle:

- TS EAMCET - 2025
- Microbiology
- The following are the parts of alimentary canal of cockroach:
I. Colon,
II. Mesenteron,
III. Crop,
IV. Gizzard,
V. Ileum,
VI. Rectum,
VII. Oesophagus
Arrange them in the correct sequence- TS EAMCET - 2025
- Respiration
- Match the following and choose the correct option from the lists given below:

- TS EAMCET - 2025
- Microbiology
- $7\hat{i}-4\hat{j}+7\hat{k}, \hat{i}-6\hat{j}+10\hat{k}, -\hat{i}-3\hat{j}+4\hat{k}, 5\hat{i}-\hat{j}+\hat{k}$ are the position vectors of the points A, B, C, D respectively. If $p\hat{i} + q\hat{j} + r\hat{k}$ is the position vector of the point of intersection of the diagonals of the quadrilateral ABCD, then $p+q+r=$
- TS EAMCET - 2025
- Vector Algebra
- If the sum of two vectors is a unit vector, then the magnitude of their difference is:
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
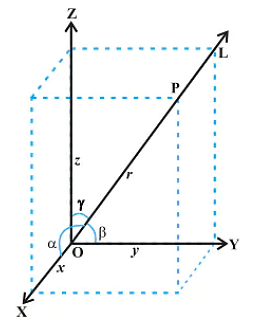
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.