Question:
The normal magnetic flux passing through a coil changes with time according to the equation $\phi = 6t^2 - 5t + 1$. What is the magnitude of the induced current at $t = 0.253\, s$ and resistance $10 \, \Omega $ ?
The normal magnetic flux passing through a coil changes with time according to the equation $\phi = 6t^2 - 5t + 1$. What is the magnitude of the induced current at $t = 0.253\, s$ and resistance $10 \, \Omega $ ?
Updated On: May 12, 2024
- 1.2 A
- 0.8 A
- 0.6 A
- 0.2 A
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Here ,
Magnetic flux, $\phi = 6t^2 - 5t + 1$
Resistance, $R = 10\, \Omega$
The induced emf is
$\varepsilon = - \frac{d\phi}{dt} = - \frac{d}{dt} \left(6t^{2} - 5t+ 1\right)=-\left(12t - 5 \right) $
At $t = 0.253 \,s$
$\varepsilon = -(12 \times 0.253 - 5 ) = 1.964 \, V = 2 V$
$\therefore$ Induced current, $ I = \frac{ \varepsilon}{R} = \frac{2}{10} = 0.2 A$
Magnetic flux, $\phi = 6t^2 - 5t + 1$
Resistance, $R = 10\, \Omega$
The induced emf is
$\varepsilon = - \frac{d\phi}{dt} = - \frac{d}{dt} \left(6t^{2} - 5t+ 1\right)=-\left(12t - 5 \right) $
At $t = 0.253 \,s$
$\varepsilon = -(12 \times 0.253 - 5 ) = 1.964 \, V = 2 V$
$\therefore$ Induced current, $ I = \frac{ \varepsilon}{R} = \frac{2}{10} = 0.2 A$
Was this answer helpful?
0
0
Top Questions on Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )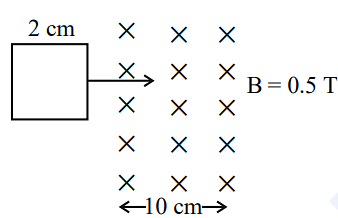
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
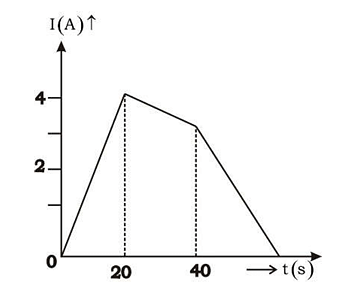
- KCET - 2021
- Physics
- Faradays laws of induction
View More Questions
Questions Asked in COMEDK UGET exam
- A $2\,kg$ mass lying on a table is displaced in the horizontal direction through $50\,cm$. The work done by the normal reaction will be
- COMEDK UGET - 2015
- work, energy and power
- The numbers of $ {H^+}$ ions present in 1 mL of a solution whose pH is 13
- COMEDK UGET - 2015
- Equilibrium
- A mixture of methylamine and dimethylamine is given to you. The reagents used to separate the components of the mixture are
- $\cot^{-1} (21) + \cot^{-1} (13) + \cot^{-1} (-8) =$
- COMEDK UGET - 2015
- Inverse Trigonometric Functions
- Pick the incorrect statement among those given below.
- COMEDK UGET - 2015
- Chemical bonding and molecular structure
View More Questions
Concepts Used:
Faradays Laws of Induction
There are two laws, given by Faraday which explain the phenomena of electromagnetic induction:
Faraday's First Law:
Whenever a conductor is placed in a varying magnetic field, an emf is induced. If the conductor circuit is closed, a current is induced, known as the induced current.
Faraday's Second Law:
The Emf induced inside a coil is equal to the rate of change of associated magnetic flux.
This law can be mathematically written as:
∈\(-N {\triangle \phi \over \triangle t}\)
