Question:
The magnetic flux linked with a coil, in webers, is given by the equation: $\phi=5 t^{2}+3 t+16$. The induced e.m.f. in the coil in the fourth second will be
The magnetic flux linked with a coil, in webers, is given by the equation: $\phi=5 t^{2}+3 t+16$. The induced e.m.f. in the coil in the fourth second will be
Updated On: Aug 1, 2022
- 145 V
- 10 V
- 210 V
- 108 V.
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
Given: Magnetic flux $(\phi)=5 t^{2}+3 t+16 .$ We know that the induced e.m.f. $(E)$
$=\frac{d \phi}{d t}=\frac{d}{d t}\left(5 t^{2}+3 t+16\right)=10 t+3 .$ Therefore induced
e.m.f.; when $t=3,\left(E_{3}\right)=(10 \times 3)+3=33\, V$
and induced e.m.f. when $t=4,\left(E_{4}\right)=(10 \times 4)+3=43 \,V$.
Therefore e.m.f. induced in the fourth $sec =E_{4}-E_{3}$ $=43-33=10\, V$
Was this answer helpful?
0
0
Top Questions on Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )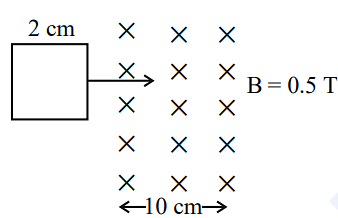
- KCET - 2023
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
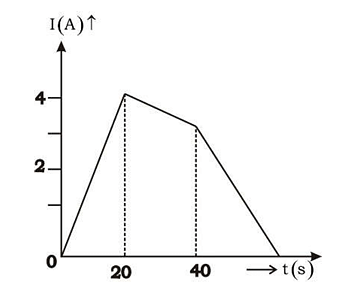
- KCET - 2021
- Physics
- Faradays laws of induction
View More Questions
Questions Asked in AIIMS exam
- The element Neodymium (Nd) belongs to the 4f series. What is its atomic number?
- AIIMS - 2024
- Modern Periodic Law And The Present Form Of The Periodic Table
- The correct increasing order of energy of orbitals in a hydrogen atom is:
- AIIMS - 2024
- Atomic Structure
- Which of the following is a globular protein?
- AIIMS - 2024
- Biomolecules
- Given that the surface charge density on a sphere is 200 μC/m2, what is the electric field at the surface of the sphere?
- AIIMS - 2024
- Electrostatics
- Which of the following is a crystalline solid?
- AIIMS - 2024
- The solid state
View More Questions
Concepts Used:
Faradays Laws of Induction
There are two laws, given by Faraday which explain the phenomena of electromagnetic induction:
Faraday's First Law:
Whenever a conductor is placed in a varying magnetic field, an emf is induced. If the conductor circuit is closed, a current is induced, known as the induced current.
Faraday's Second Law:
The Emf induced inside a coil is equal to the rate of change of associated magnetic flux.
This law can be mathematically written as:
∈\(-N {\triangle \phi \over \triangle t}\)
