Let y = y1(x) and y = y2(x) be two distinct solution of the differential equation
\(\frac{dy}{dx} = x+y,\)
with y1(0) = 0 and y2(0) = 1 respectively. Then, the number of points of intersection of y = y1 (x) and y = y2(x) is
Let y = y1(x) and y = y2(x) be two distinct solution of the differential equation
\(\frac{dy}{dx} = x+y,\)
with y1(0) = 0 and y2(0) = 1 respectively. Then, the number of points of intersection of y = y1 (x) and y = y2(x) is
- 0
- 1
- 2
- 3
The Correct Option is A
Solution and Explanation
The correct answer \(\frac{dy}{dx}\) is (A):
\(\frac{dy}{dx} = x+y\)
Let x + y = t
1+\(\frac{dy}{dx}\)=\(\frac{dt}{dx}\)
\(\frac{dt}{dx}\)-1 = t
⇒ ∫\(\frac{dt}{t}\)+1 = ∫dx
In |t+1| = x+C'
|t+1|=Cex
|x+y+1| = Cex
For y1 (x),y1(0) = 0
⇒ C = 1
For y2 (x),y2(0) = 1
⇒ C = 2
y1(x) is given by |x+y+1| = ex
y2(x) is given by |x+y+1| = 2ex
At point of intersection
ex = 2ex
No solution
So, there is no point of intersection of y1(x) and y2(x).
Top Questions on Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of the integral: ∫ (2x + 3)/((xy)(x^2 + 1)) dx
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam

In the given circuit the sliding contact is pulled outwards such that the electric current in the circuit changes at the rate of 8 A/s. At an instant when R is 12 Ω, the value of the current in the circuit will be A.- JEE Main - 2025
- Electrical Circuits
- Let \( \vec{a} = \hat{i} + 2\hat{j} + \hat{k} \) and \( \vec{b} = 2\hat{i} + 7\hat{j} + 3\hat{k} \). Let \( L_1 : \vec{r} = (-\hat{i} + 2\hat{j} + \hat{k}) + \lambda \vec{a}, \lambda \in {R} \) and \( L_2 : \vec{r} = (\hat{j} + \hat{k}) + \mu \vec{b}, \mu \in \mathbb{R} \) be two lines. If the line \( L_3 \) passes through the point of intersection of \( L_1 \) and \( L_2 \), and is parallel to \( \vec{a} + \vec{b} \), then \( L_3 \) passes through the point:
- JEE Main - 2025
- Vectors
Let $ P_n = \alpha^n + \beta^n $, $ n \in \mathbb{N} $. If $ P_{10} = 123,\ P_9 = 76,\ P_8 = 47 $ and $ P_1 = 1 $, then the quadratic equation having roots $ \alpha $ and $ \frac{1}{\beta} $ is:
- JEE Main - 2025
- Relations and functions
For $ \alpha, \beta, \gamma \in \mathbb{R} $, if $$ \lim_{x \to 0} \frac{x^2 \sin \alpha x + (\gamma - 1)e^{x^2} - 3}{\sin 2x - \beta x} = 3, $$ then $ \beta + \gamma - \alpha $ is equal to:
The maximum speed of a boat in still water is 27 km/h. Now this boat is moving downstream in a river flowing at 9 km/h. A man in the boat throws a ball vertically upwards with speed of 10 m/s. Range of the ball as observed by an observer at rest on the river bank is _________ cm. (Take \( g = 10 \, {m/s}^2 \)).
- JEE Main - 2025
- System of Particles & Rotational Motion
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
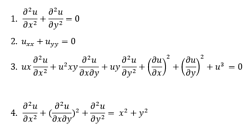
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
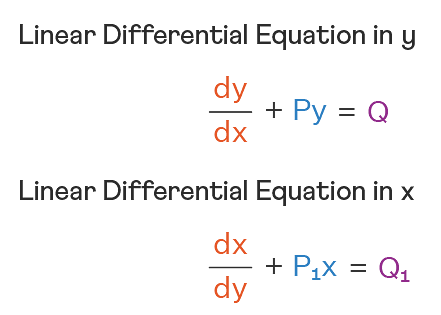
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations