Let the plane
\(P : \stackrel{→}{r} . \stackrel{→}{a} = d\)
contain the line of intersection of two planes
\(\stackrel{→}{r} . ( \hat{i} + 3\hat{j} - \hat{k} ) = 6\)
and
\(\stackrel{→}{r} . ( -6\hat{i} + 5\hat{j} - \hat{k} ) = 7\)
. If the plane P passes through the point (2, 3, 1/2),
then the value of \(\frac{| 13a→|² }{d²}\) is equal to
Let the plane
\(P : \stackrel{→}{r} . \stackrel{→}{a} = d\)
contain the line of intersection of two planes
\(\stackrel{→}{r} . ( \hat{i} + 3\hat{j} - \hat{k} ) = 6\)
and
\(\stackrel{→}{r} . ( -6\hat{i} + 5\hat{j} - \hat{k} ) = 7\)
. If the plane P passes through the point (2, 3, 1/2),
then the value of \(\frac{| 13a→|² }{d²}\) is equal to
- 90
- 93
- 95
- 97
The Correct Option is B
Solution and Explanation
The correct answer is (B) : 93
P1: x + 3y – z = 6
P2: –6x + 5y – z = 7
Family of planes passing through line of intersection of P1 and P2 is given by x(1 – 6λ) + y(3 + 5λ) + z (–1 – λ) – (6 + 7λ) = 0
It passes through (2, 3, 1/2)
So,
\(2 ( 1 - 6λ ) + 3(3 + 5λ) + \frac{1}{2} (-1 - λ) - ( 6 + 7λ ) = 0\)
\(⇒ 2 - 12λ + 9 + 15λ - \frac{1}{2} - \frac{λ}{2} - 6 - 7λ = 0\)
\(⇒ \frac{9}{2} - \frac{9λ}{2} = 0 ⇒ λ = 1\)
Required plane is
–5x + 8y – 2z – 13 = 0
Or
\(\stackrel{→}{r} . ( -5\hat{i} + 8\hat{j} - 2\hat{k} ) = 13\)
\(\frac{| 13a→ |²}{ |d|²} = \frac{13²}{(13)²} . |\stackrel{→}{a}|^2 = 93\)
Top Questions on Three Dimensional Geometry
- If the distances of the point \( (1,2,a) \) from the line \[ \frac{x-1}{1}=\frac{y}{2}=\frac{z-1}{1} \] along the lines \[ L_1:\ \frac{x-1}{3}=\frac{y-2}{4}=\frac{z-a}{b} \quad \text{and} \quad L_2:\ \frac{x-1}{1}=\frac{y-2}{4}=\frac{z-a}{c} \] are equal, then \( a+b+c \) is equal to:
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
- The value of the integral \( \int_{\frac{\pi}{24}}^{\frac{5\pi}{24}} \frac{dx}{1 + \sqrt[3]{\tan 2x}} \) is :
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
Let the lines $L_1 : \vec r = \hat i + 2\hat j + 3\hat k + \lambda(2\hat i + 3\hat j + 4\hat k)$, $\lambda \in \mathbb{R}$ and $L_2 : \vec r = (4\hat i + \hat j) + \mu(5\hat i + + 2\hat j + \hat k)$, $\mu \in \mathbb{R}$ intersect at the point $R$. Let $P$ and $Q$ be the points lying on lines $L_1$ and $L_2$, respectively, such that $|PR|=\sqrt{29}$ and $|PQ|=\sqrt{\frac{47}{3}}$. If the point $P$ lies in the first octant, then $27(QR)^2$ is equal to}
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
- Let a line $L$ passing through the point $P(1,1,1)$ be perpendicular to the lines \[ \frac{x-4}{4}=\frac{y-1}{1}=\frac{z-1}{1} \quad \text{and} \quad \frac{x-17}{1}=\frac{y-71}{1}=\frac{z}{0}. \] Let the line $L$ intersect the $yz$-plane at the point $Q$.
Another line parallel to $L$ and passing through the point $S(1,0,-1)$ intersects the $yz$-plane at the point $R$.
Then the square of the area of the parallelogram $PQRS$ is equal to
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
- Let \( L \) be the line \[ \frac{x+1}{2} = \frac{y+1}{3} = \frac{z+3}{6} \] and let \( S \) be the set of all points \( (a,b,c) \) on \( L \), whose distance from the line \[ \frac{x+1}{2} = \frac{y+1}{3} = \frac{z-9}{0} \] along the line \( L \) is \( 7 \). Then \[ \sum_{(a,b,c)\in S} (a+b+c) \] is equal to
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
Questions Asked in JEE Main exam
- The system of linear equations
$x + y + z = 6$
$2x + 5y + az = 36$
$x + 2y + 3z = b$
has- JEE Main - 2026
- Matrices and Determinants
- The displacement of a particle executing simple harmonic motion with time period \(T\) is expressed as \[ x(t)=A\sin\omega t, \] where \(A\) is the amplitude of oscillation. If the maximum value of the potential energy of the oscillator is found at \[ t=\frac{T}{2\beta}, \] then the value of \(\beta\) is ________.
- JEE Main - 2026
- Waves and Oscillations
- A complex number 'z' satisfy both \(|z-6|=5\) & \(|z+2-6i|=5\) simultaneously. Find the value of \(z^3 + 3z^2 - 15z + 141\).
- JEE Main - 2026
- Algebra
In the given figure, the blocks $A$, $B$ and $C$ weigh $4\,\text{kg}$, $6\,\text{kg}$ and $8\,\text{kg}$ respectively. The coefficient of sliding friction between any two surfaces is $0.5$. The force $\vec{F}$ required to slide the block $C$ with constant speed is ___ N.
(Given: $g = 10\,\text{m s}^{-2}$)
- JEE Main - 2026
- Rotational Mechanics
Two circular discs of radius \(10\) cm each are joined at their centres by a rod, as shown in the figure. The length of the rod is \(30\) cm and its mass is \(600\) g. The mass of each disc is also \(600\) g. If the applied torque between the two discs is \(43\times10^{-7}\) dyne·cm, then the angular acceleration of the system about the given axis \(AB\) is ________ rad s\(^{-2}\).

- JEE Main - 2026
- Rotational motion
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
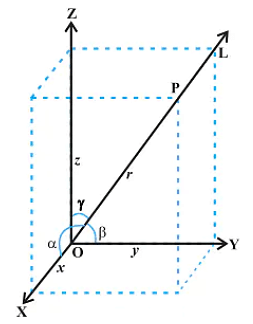
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.