Let R1 and R2 be two relations defined on ℝ by a R1b ⇔ ab ≥ 0 and aR2b ⇔ a ≥ b. Then,
- R1 is an equivalence relation but not R2
- R2 is an equivalence relation but not R1
- Both R1 and R2 are equivalence relations
- Neither R1 nor R2 is an equivalence relation
The Correct Option is D
Solution and Explanation
The correct answer is (D):
aR1b ⇔ ab ≥ 0
So, definitely (a, a) ∈ R1 as a2 ≥ 0
If (a, b) ∈ R1 ⇒ (b, a) ∈ R1
But if (a, b) ∈ R1, (b, c) ∈ R1
⇒ Then (a, c) may or may not belong to R1
{Consider a = –5, b = 0, c = 5 so (a, b) and (b, c) ∈ R1 but ac < 0}
So, R1 is not equivalence relation
a R2 b ⇔ a ≥ b
(a, a) ∈ R2 ⇒ so reflexive relation
If (a, b) ∈ R2 then (b, a) may or may not belong to R2
⇒ So not symmetric
Hence it is not equivalence relation
Top Questions on Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- If $\frac{x+3}{(x+1)(x^2+2)} = \frac{a}{x+1} + \frac{bx+c}{x^2+2}$ then $a-b+c =$
- TS EAMCET - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
Given below are two statements I and II.
Statement I: Dumas method is used for estimation of "Nitrogen" in an organic compound.
Statement II: Dumas method involves the formation of ammonium sulfate by heating the organic compound with concentrated H\(_2\)SO\(_4\). In the light of the above statements, choose the correct answer from the options given below:- JEE Main - 2025
- Nitrogen
Considering Bohr’s atomic model for hydrogen atom :
(A) the energy of H atom in ground state is same as energy of He+ ion in its first excited state.
(B) the energy of H atom in ground state is same as that for Li++ ion in its second excited state.
(C) the energy of H atom in its ground state is same as that of He+ ion for its ground state.
(D) the energy of He+ ion in its first excited state is same as that for Li++ ion in its ground state.- JEE Main - 2025
- Atomic Models
- In an adiabatic process, which of the following statements is true?
- JEE Main - 2025
- Thermodynamics
- To obtain the given truth table, the following logic gate should be placed at G

- JEE Main - 2025
- Logic gates
- Choose the correct logic circuit for the given truth table having inputs A and B.

- JEE Main - 2025
- Logic gates
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
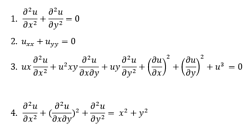
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
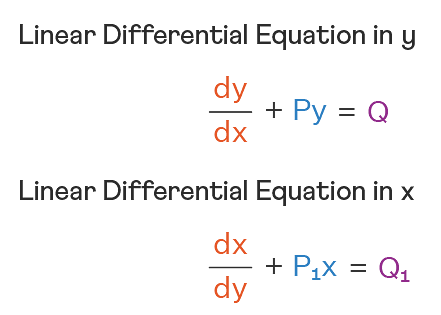
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations