Let P(a, b) be a point on the parabola y2 = 8x such that the tangent at P passes through the centre of the circle x2 + y2 – 10x – 14y + 65 = 0. Let A be the product of all possible values of a and B be the product of all possible values of b. Then the value of A + B is equal to
- 0
- 25
- 40
- 65
The Correct Option is D
Solution and Explanation
The correct answer is (D):
Centre of circle x2 + y2 – 10x –14y + 65 = 0 is at (5, 7).
Let the equation of tangent to y2 = 8x is
yt = x + 2t2
which passes through (5, 7)
7t = 5 + 2t2
⇒ 2t2 – 7t + 5 = 0
t = 1, \(\frac{5}{2}\)
A = 1×12×2×(\(\frac{5}{2}\))2
= 25
B = 2×2×1×2×2×\(\frac{5}{2}\)
= 40
A+B = 65
Top Questions on Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of the integral: ∫ (2x + 3)/((xy)(x^2 + 1)) dx
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- A force of 49 N acts tangentially at the highest point of a sphere (solid of mass 20 kg) kept on a rough horizontal plane. If the sphere rolls without slipping, then the acceleration of the center of the sphere is:
- JEE Main - 2025
- Quantum Mechanics
Let \( A = \{-3, -2, -1, 0, 1, 2, 3\} \). A relation \( R \) is defined such that \( xRy \) if \( y = \max(x, 1) \). The number of elements required to make it reflexive is \( l \), the number of elements required to make it symmetric is \( m \), and the number of elements in the relation \( R \) is \( n \). Then the value of \( l + m + n \) is equal to:
- JEE Main - 2025
- Sets and Relations
For hydrogen-like species, which of the following graphs provides the most appropriate representation of \( E \) vs \( Z \) plot for a constant \( n \)?
[E : Energy of the stationary state, Z : atomic number, n = principal quantum number]- JEE Main - 2025
- Hydrogen
- Concentrated nitric acid is labelled as 75%by mass. The volume in mL of the solution which contains 30 g of nitric acid is: Given: Density of nitric acid solution is 1.25 g/mL.
- JEE Main - 2025
- Solutions
The number of 6-letter words, with or without meaning, that can be formed using the letters of the word MATHS such that any letter that appears in the word must appear at least twice, is $ 4 \_\_\_\_\_$.
- JEE Main - 2025
- permutations and combinations
JEE Main Notification
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
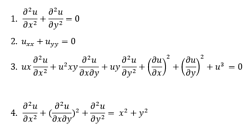
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
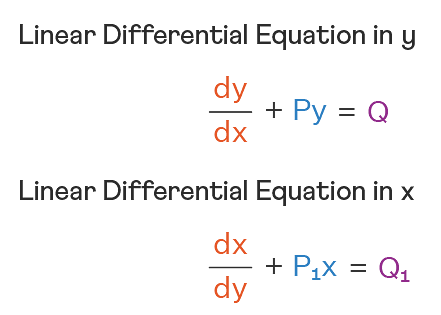
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations