Let m1, m2 be the slopes of two adjacent sides of a square of side a such that \(a^2 + 11a + 3(m_1^2 + m_2^2) = 220\). If one vertex of the square is \((10(\cos \alpha - \sin \alpha), 10(\sin \alpha + \cos \alpha))\), where \(\alpha \in \left(0, \frac{\pi}{2}\right)\)and the equation of one diagonal is \((\cos \alpha - \sin \alpha)x + (\sin \alpha + \cos \alpha)y = 10\), then \(72(\sin^4 \alpha + \cos^4 \alpha) + a^2 - 3a + 13\) is equal to :
- 119
- 128
- 145
- 155
The Correct Option is B
Solution and Explanation
One vertex of square is
\((10(\cos \alpha - \sin \alpha), 10(\sin \alpha + \cos \alpha))\)
and one of the diagonal is
\((\cos \alpha - \sin \alpha)x + (\sin \alpha + \cos \alpha)y = 10\)
So the other diagonal can be obtained as
\((\cos \alpha + \sin \alpha)x - (\cos \alpha - \sin \alpha)y = 0\)
So, point of intersection of diagonal will be
\((5(\cos \alpha - \sin \alpha), 5(\cos \alpha + \sin \alpha))\)
Therefore, the vertex opposite to the given vertex is (0, 0).
So, the diagonal length
\(10\sqrt{2}\)
Side length \((a) = 10\)
It is given that
\(a^2 + 11a + 3(m_1^2 + m_2^2) = 220\)
\(m_1^2 + m_2^2 = 220 - 100 - 110 = 103\)
and \(m_1 \cdot m_2 = -1\)
Slopes of the sides are \(\tan \alpha \quad \text{and} \quad -\cot \alpha\)
\(\tan(2\alpha) = 3 \quad \text{or} \quad \tan(2\alpha) = \frac{1}{3}\)
\(72(\sin 4\alpha + \cos 4\alpha) + a^2 - 3a + 13\)
\(72 \cdot \tan^4 \alpha + \frac{1}{{(1 + \tan^2 \alpha)}^2} + a^2 - 3a + 13 = 128\)
So, the correct option is (B): \(128\)
Top Questions on Integration by Partial Fractions
- If $\frac{x+3}{(x+1)(x^2+2)} = \frac{a}{x+1} + \frac{bx+c}{x^2+2}$ then $a-b+c =$
- TS EAMCET - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- A 400 g solid cube having an edge of length \(10\) cm floats in water. How much volume of the cube is outside the water? (Given: density of water = \(1000 { kg/m}^3\))
Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): The density of the copper ($^{64}Cu$) nucleus is greater than that of the carbon ($^{12}C$) nucleus.
Reason (R): The nucleus of mass number A has a radius proportional to $A^{1/3}$.
In the light of the above statements, choose the most appropriate answer from the options given below:- JEE Main - 2025
- Nuclear physics
- The roots of the quadratic equation \( 3x^2 - px + q = 0 \) are the 10th and 11th terms of an arithmetic progression with common difference \( \frac{3}{2} \). If the sum of the first 11 terms of this arithmetic progression is 88, then \( q - 2q \) is equal to:
- JEE Main - 2025
- Arithmetic Progression and Quadratic Equations
- The type of oxide formed by the element among Li, Na, Be, Mg, B and Al that has the least atomic radius is:
- JEE Main - 2025
- Periodicity of Elements
- The number of real solution(s) of the equation \( x^2 + 3x + 2 = \min \left( |x - 3|, |x + 2| \right) \) is:
- JEE Main - 2025
- Coordinate Geometry
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
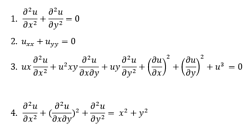
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
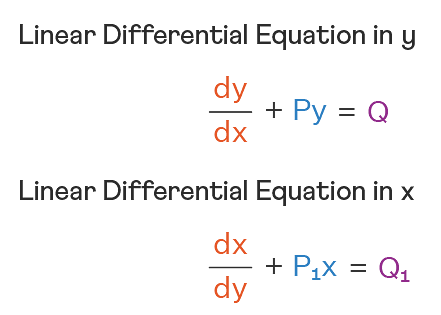
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations