Question:
Electric field in a region is given by
\[
\vec{E} = A x\,\hat{i} + B y\,\hat{j},
\]
where \( A = 10 \,\text{V/m}^2 \) and \( B = 5 \,\text{V/m}^2 \). If the electric potential at a point \( (10, 20) \) is \(500\ \text{V}\), then the electric potential at origin is __________ V.
Electric field in a region is given by
\[
\vec{E} = A x\,\hat{i} + B y\,\hat{j},
\]
where \( A = 10 \,\text{V/m}^2 \) and \( B = 5 \,\text{V/m}^2 \). If the electric potential at a point \( (10, 20) \) is \(500\ \text{V}\), then the electric potential at origin is __________ V.
Show Hint
Electric potential can be obtained by integrating the electric field components with proper constants of integration.
Updated On: Feb 4, 2026
- \(1000\)
- \(500\)
- \(2000\)
- \(0\)
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
The electric field is related to potential by
\[
\vec{E} = -\nabla V.
\]
Step 1: Write component-wise relations.
\[ E_x = -\frac{\partial V}{\partial x} = A x, \quad E_y = -\frac{\partial V}{\partial y} = B y. \] Thus, \[ \frac{\partial V}{\partial x} = -A x, \quad \frac{\partial V}{\partial y} = -B y. \]
Step 2: Integrate to find potential.
Integrating with respect to \(x\), \[ V = -\frac{A x^2}{2} + f(y). \] Differentiating with respect to \(y\), \[ \frac{\partial V}{\partial y} = f'(y) = -B y. \] Integrating, \[ f(y) = -\frac{B y^2}{2} + C. \] Hence, \[ V(x,y) = -\frac{A x^2}{2} - \frac{B y^2}{2} + C. \]
Step 3: Use given potential value.
At \( (10,20) \), \[ 500 = -\frac{10(10)^2}{2} - \frac{5(20)^2}{2} + C. \] \[ 500 = -500 - 1000 + C. \] \[ C = 2000. \] Thus, potential at origin is \[ V(0,0) = 2000 - 0 - 0 = 1000\ \text{V}. \]
Final Answer: \[ \boxed{1000} \]
Step 1: Write component-wise relations.
\[ E_x = -\frac{\partial V}{\partial x} = A x, \quad E_y = -\frac{\partial V}{\partial y} = B y. \] Thus, \[ \frac{\partial V}{\partial x} = -A x, \quad \frac{\partial V}{\partial y} = -B y. \]
Step 2: Integrate to find potential.
Integrating with respect to \(x\), \[ V = -\frac{A x^2}{2} + f(y). \] Differentiating with respect to \(y\), \[ \frac{\partial V}{\partial y} = f'(y) = -B y. \] Integrating, \[ f(y) = -\frac{B y^2}{2} + C. \] Hence, \[ V(x,y) = -\frac{A x^2}{2} - \frac{B y^2}{2} + C. \]
Step 3: Use given potential value.
At \( (10,20) \), \[ 500 = -\frac{10(10)^2}{2} - \frac{5(20)^2}{2} + C. \] \[ 500 = -500 - 1000 + C. \] \[ C = 2000. \] Thus, potential at origin is \[ V(0,0) = 2000 - 0 - 0 = 1000\ \text{V}. \]
Final Answer: \[ \boxed{1000} \]
Was this answer helpful?
0
0
Top Questions on Electric Potential And Potential Difference
Resistance of each side is $R$. Find equivalent resistance between two opposite points as shown in the figure.

- JEE Main - 2026
- Physics
- Electric Potential And Potential Difference
- If a particle of mass 10 mg and charge 2 µC at rest is subjected to a uniform electric field of potential difference 160 V, then the velocity acquired by the particle is
- TS EAMCET - 2025
- Physics
- Electric Potential And Potential Difference
- A charge of 10 coulomb is brought from infinity to a point \( P \) near a charged body and in this process 200 joules of work is done. Electric potential at point \( P \) is:
- JEECUP - 2024
- Physics
- Electric Potential And Potential Difference
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)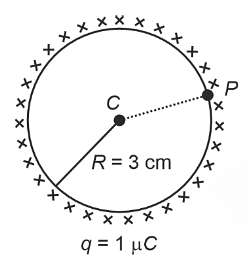
- NEET (UG) - 2024
- Physics
- Electric Potential And Potential Difference
- Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
- COMEDK UGET - 2023
- Physics
- Electric Potential And Potential Difference
View More Questions
Questions Asked in JEE Main exam
Two point charges 2q and q are placed at vertex A and centre of face CDEF of the cube as shown in figure. The electric flux passing through the cube is :

- JEE Main - 2026
- Rotational motion
An object is projected with kinetic energy K from point A at an angle 60° with the horizontal. The ratio of the difference in kinetic energies at points B and C to that at point A (see figure), in the absence of air friction is :

- JEE Main - 2026
- Current electricity
- Consider the following two first-order reactions: A \(\to\) B (first reaction) C \(\to\) D (second reaction) The rate constant for first reaction at 500 K is double of the same at 300 K. At 500 K, 50% of the reaction becomes complete in 2 hours. The activation energy of the second reaction is half of that of first reaction. If the rate constant at 500 K of the second reaction becomes double of the rate constant of first reaction at the same temperature; then rate constant for the second reaction at 300 K is ______ \(\times 10^{-3}\,\text{hour}^{-1}\) (nearest integer).
- JEE Main - 2026
- Organic Chemistry
- A volume of \(x\) mL of 5 M NaHCO\(_3\) solution was mixed with 10 mL of 2 M H\(_2\)CO\(_3\) solution to make an electrolytic buffer. If the same buffer was used in the following electrochemical cell to record a cell potential of 253.5 mV, then the value of \(x =\) ______ mL (nearest integer). \[ \ce{Sn(s) | Sn(OH)2(s) | HSnO2^- (0.05 M) | OH^- (0.05 M) || Bi2O3(s) | Bi(s)} \] Given: \[ E^\circ(\ce{HSnO2^- / Sn(OH)2}) = -0.90 \,\text{V}, \quad E^\circ(\ce{Bi2O3 / Bi}) = -0.44 \,\text{V} \] \[ pK_a(\ce{H2CO3}) = 6.11, \quad \frac{2.303RT}{F} = 0.059 \,\text{V}, \quad \text{Antilog}(1.29) = 19.5 \]
- JEE Main - 2026
- Electrochemistry
- The number of isoelectronic species among \(\ce{S^{2-}}, \ce{C^{4-}}, \ce{Mn^{2+}}, \ce{Co^{3+}}\) and \(\ce{Fe^{3+}}\) is ‘n’. If ‘n’ moles of AgCl is formed during the reaction of complex with formula \(\ce{CoCl2(en)2NH3\) with excess of AgNO\(_3\) solution, then the number of electrons present in the \(t_{2g}\) orbital of the complex is ________.}
- JEE Main - 2026
- Organic Chemistry
View More Questions