Question:
If a particle of mass 10 mg and charge 2 µC at rest is subjected to a uniform electric field of potential difference 160 V, then the velocity acquired by the particle is
If a particle of mass 10 mg and charge 2 µC at rest is subjected to a uniform electric field of potential difference 160 V, then the velocity acquired by the particle is
Show Hint
Always convert all given quantities to their base SI units (mass to kg, charge to C, etc.) before substituting them into formulas. This prevents unit-related errors in the final calculation.
Updated On: Oct 17, 2025
- 9 ms⁻¹
- 4 ms⁻¹
- 6 ms⁻¹
- 8 ms⁻¹
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Step 1: Understanding the Concept:
This problem applies the Work-Energy Theorem. When a charged particle is accelerated by an electric field through a potential difference, the work done by the electric field on the particle is converted into its kinetic energy.
Step 2: Key Formula or Approach:
The work done (\(W\)) by the electric field on a charge (\(q\)) moving through a potential difference (\(\Delta V\)) is given by:
\[ W = q \Delta V \] The change in kinetic energy (\(\Delta K\)) of the particle is:
\[ \Delta K = K_f - K_i = \frac{1}{2}mv^2 - \frac{1}{2}mu^2 \] According to the Work-Energy Theorem, \(W = \Delta K\).
Step 3: Detailed Explanation:
First, we list the given values in SI units:
- Mass, \(m = 10 \text{ mg} = 10 \times 10^{-3} \text{ g} = 10 \times 10^{-6} \text{ kg}\).
- Charge, \(q = 2 \text{ µC} = 2 \times 10^{-6} \text{ C}\).
- Potential difference, \(\Delta V = 160 \text{ V}\).
- The particle starts from rest, so its initial velocity, \(u = 0\).
Now, we apply the Work-Energy Theorem:
\[ q \Delta V = \frac{1}{2}mv^2 - \frac{1}{2}m(0)^2 \] \[ q \Delta V = \frac{1}{2}mv^2 \] We rearrange the formula to solve for the final velocity, \(v\):
\[ v^2 = \frac{2q \Delta V}{m} \] Substitute the given values:
\[ v^2 = \frac{2 \times (2 \times 10^{-6} \text{ C}) \times (160 \text{ V})}{10 \times 10^{-6} \text{ kg}} \] The \(10^{-6}\) terms in the numerator and denominator cancel out.
\[ v^2 = \frac{2 \times 2 \times 160}{10} = \frac{640}{10} = 64 \] Now, take the square root to find the velocity:
\[ v = \sqrt{64} = 8 \text{ m/s} \] Step 4: Final Answer:
The velocity acquired by the particle is 8 ms⁻¹. Therefore, option (D) is correct.
This problem applies the Work-Energy Theorem. When a charged particle is accelerated by an electric field through a potential difference, the work done by the electric field on the particle is converted into its kinetic energy.
Step 2: Key Formula or Approach:
The work done (\(W\)) by the electric field on a charge (\(q\)) moving through a potential difference (\(\Delta V\)) is given by:
\[ W = q \Delta V \] The change in kinetic energy (\(\Delta K\)) of the particle is:
\[ \Delta K = K_f - K_i = \frac{1}{2}mv^2 - \frac{1}{2}mu^2 \] According to the Work-Energy Theorem, \(W = \Delta K\).
Step 3: Detailed Explanation:
First, we list the given values in SI units:
- Mass, \(m = 10 \text{ mg} = 10 \times 10^{-3} \text{ g} = 10 \times 10^{-6} \text{ kg}\).
- Charge, \(q = 2 \text{ µC} = 2 \times 10^{-6} \text{ C}\).
- Potential difference, \(\Delta V = 160 \text{ V}\).
- The particle starts from rest, so its initial velocity, \(u = 0\).
Now, we apply the Work-Energy Theorem:
\[ q \Delta V = \frac{1}{2}mv^2 - \frac{1}{2}m(0)^2 \] \[ q \Delta V = \frac{1}{2}mv^2 \] We rearrange the formula to solve for the final velocity, \(v\):
\[ v^2 = \frac{2q \Delta V}{m} \] Substitute the given values:
\[ v^2 = \frac{2 \times (2 \times 10^{-6} \text{ C}) \times (160 \text{ V})}{10 \times 10^{-6} \text{ kg}} \] The \(10^{-6}\) terms in the numerator and denominator cancel out.
\[ v^2 = \frac{2 \times 2 \times 160}{10} = \frac{640}{10} = 64 \] Now, take the square root to find the velocity:
\[ v = \sqrt{64} = 8 \text{ m/s} \] Step 4: Final Answer:
The velocity acquired by the particle is 8 ms⁻¹. Therefore, option (D) is correct.
Was this answer helpful?
0
0
Top Questions on Electric Potential And Potential Difference
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)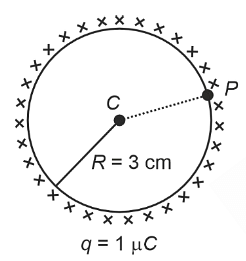
- NEET (UG) - 2024
- Physics
- Electric Potential And Potential Difference
- A charge of 10 coulomb is brought from infinity to a point \( P \) near a charged body and in this process 200 joules of work is done. Electric potential at point \( P \) is:
- JEECUP - 2024
- Physics
- Electric Potential And Potential Difference
- Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
- COMEDK UGET - 2023
- Physics
- Electric Potential And Potential Difference
- Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
- Electric potential at a point \( P \) due to a point charge of \( 5 \times 10^{-9} \, \text{C} \) is \( 50 \, \text{V} \). The distance of \( P \) from the point charge is:
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
View More Questions
Questions Asked in TS EAMCET exam
- If the sum of two vectors is a unit vector, then the magnitude of their difference is:
- Arrange the following in the increasing order of oxidation number of nitrogen
A. N$_2$O
B. NO$_3^-$
C. NO
D. NO$_2$- TS EAMCET - 2025
- Chemistry in Everyday Life
- Identify the correct matching pair to Calvin cycle:

- TS EAMCET - 2025
- Microbiology
- The following are the parts of alimentary canal of cockroach:
I. Colon,
II. Mesenteron,
III. Crop,
IV. Gizzard,
V. Ileum,
VI. Rectum,
VII. Oesophagus
Arrange them in the correct sequence- TS EAMCET - 2025
- Respiration
- Match the following and choose the correct option from the lists given below:

- TS EAMCET - 2025
- Microbiology
View More Questions