Question:
Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
Show Hint
When the electric potential is zero due to two point charges, the magnitudes of the potentials due to both charges must be equal but opposite in sign. Set the sum of the potentials equal to zero and solve for the distance.
Updated On: May 8, 2025
- 0.5 m from the charge \( 10 \, \mu C \)
- 0.76 m from the charge \( 20 \, \mu C \)
- 0.67 m from the charge \( 20 \, \mu C \)
- 0.25 m from the charge \( 10 \, \mu C \)
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The electric potential at a point due to a point charge is given by the formula:
\[
V = \frac{kQ}{r}
\]
Where:
- \( V \) is the electric potential,
- \( k \) is Coulomb's constant (\( 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \)),
- \( Q \) is the charge,
- \( r \) is the distance from the charge.
At the point where the potential is zero, the potentials due to both charges must cancel each other out. Therefore, the total electric potential at that point is zero:
\[
V_1 + V_2 = 0
\]
For the two charges:
- The charge \( Q_1 = 20 \, \mu C \) is at a distance \( r_1 \) from the point where the potential is zero.
- The charge \( Q_2 = -10 \, \mu C \) is at a distance \( r_2 = 1 - r_1 \) from the same point.
The electric potentials at the point due to the charges are:
\[
\frac{k \times 20 \times 10^{-6}}{r_1} + \frac{k \times (-10 \times 10^{-6})}{(1 - r_1)} = 0
\]
Simplifying this equation:
\[
\frac{20 \times 10^{-6}}{r_1} = \frac{10 \times 10^{-6}}{(1 - r_1)}
\]
\[
\frac{20}{r_1} = \frac{10}{1 - r_1}
\]
Cross-multiply to solve for \( r_1 \):
\[
20(1 - r_1) = 10r_1
\]
\[
20 - 20r_1 = 10r_1
\]
\[
20 = 30r_1
\]
\[
r_1 = \frac{20}{30} = 0.67 \, \text{m}
\]
Thus, the electric potential is zero at a point 0.67 m from the \( 20 \, \mu C \) charge.
Was this answer helpful?
0
0
Top Questions on Electric Potential And Potential Difference
- If a particle of mass 10 mg and charge 2 µC at rest is subjected to a uniform electric field of potential difference 160 V, then the velocity acquired by the particle is
- TS EAMCET - 2025
- Physics
- Electric Potential And Potential Difference
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)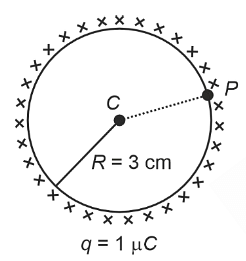
- NEET (UG) - 2024
- Physics
- Electric Potential And Potential Difference
- A charge of 10 coulomb is brought from infinity to a point \( P \) near a charged body and in this process 200 joules of work is done. Electric potential at point \( P \) is:
- JEECUP - 2024
- Physics
- Electric Potential And Potential Difference
- Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
- Electric potential at a point \( P \) due to a point charge of \( 5 \times 10^{-9} \, \text{C} \) is \( 50 \, \text{V} \). The distance of \( P \) from the point charge is:
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
View More Questions
Questions Asked in COMEDK UGET exam
- The magnetic flux linked with a coil is given by the equation: $ \phi = 8t^2 + t + 10 $ The e.m.f. induced in the coil in the 3rd second will be
- COMEDK UGET - 2024
- Electromagnetic induction
- A satellite is revolving around the earth in a circular orbit with kinetic energy of $1.69 \times 10^{10}$ J. The additional kinetic energy required for just escaping into the outer space is
- COMEDK UGET - 2024
- Escape Speed
A solid cylinder of mass 2 kg and radius 0.2 m is rotating about its own axis without friction with angular velocity 5 rad/s. A particle of mass 1 kg moving with a velocity of 5 m/s strikes the cylinder and sticks to it as shown in figure.

The angular velocity of the system after the particle sticks to it will be:- COMEDK UGET - 2024
- The Angular Momentum
- In a given semiconductor, the ratio of the number density of electron to number density of hole is 2 : 1. If $ \frac{1}{7} $th of the total current is due to the hole and the remaining is due to the electrons, the ratio of the drift velocity of holes to the drift velocity of electrons is :
- COMEDK UGET - 2024
- Semiconductors
- A transformer which steps down 330 V to 33 V is to operate a device having impedance 110 $\Omega$. The current drawn by the primary coil of the transformer is:
- COMEDK UGET - 2024
- Transformers
View More Questions