A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)
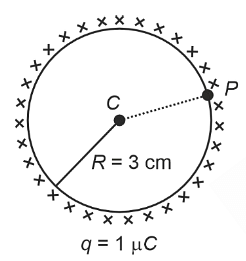
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)

- 3 × 105
- 1 × 105
- 0.5 × 105
- Zero
The Correct Option is D
Approach Solution - 1
To determine the potential difference between two points \( C \) and \( P \) on a charged thin spherical shell, we need to consider the properties of potential inside and outside the shell. For a thin spherical shell:
- Inside the shell (any point within the radius of the shell), the electric potential is constant. This is because the electric field inside the shell is zero due to the symmetry and Gauss's law. Therefore, the potential difference between any two points inside the shell is zero.
- Outside the shell, the shell behaves as a point charge located at its center. The potential \( V \) at a distance \( r \) from the center is given by \( V = \frac{kQ}{r} \), where \( Q \) is the total charge on the shell, and \( k = 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \).
- If the points \( C \) and \( P \) are both either inside or at the same radius from the center of the shell, the potential difference between them is zero.
Given that both points are either inside the shell or at the same radial distance, the potential difference is: Zero
Approach Solution -2
Step 1: Recall the Property of a Spherical Shell
Inside a charged spherical shell, the electric field is zero due to the symmetry of the charge distribution. Hence, the potential remains constant inside the shell.
Step 2: Potential Difference Between C and P
Since the electric field is zero inside the shell, the potential at any two points inside the shell, including C and P, is the same:
$$ V_C = V_P, \quad \Delta V = V_C - V_P = 0 $$
Step 3: Conclude
The potential difference between C and P is 0V.
Top Questions on Electric Potential And Potential Difference
- If a particle of mass 10 mg and charge 2 µC at rest is subjected to a uniform electric field of potential difference 160 V, then the velocity acquired by the particle is
- TS EAMCET - 2025
- Physics
- Electric Potential And Potential Difference
- A charge of 10 coulomb is brought from infinity to a point \( P \) near a charged body and in this process 200 joules of work is done. Electric potential at point \( P \) is:
- JEECUP - 2024
- Physics
- Electric Potential And Potential Difference
- Two point charges \( 20 \, \mu C \) and \( -10 \, \mu C \) are separated by a distance of 1 m in air. At what point on the line joining the two charges, the electric potential is zero.
- COMEDK UGET - 2023
- Physics
- Electric Potential And Potential Difference
- Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
- Electric potential at a point \( P \) due to a point charge of \( 5 \times 10^{-9} \, \text{C} \) is \( 50 \, \text{V} \). The distance of \( P \) from the point charge is:
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
Questions Asked in NEET exam
A bob of heavy mass \(m\) is suspended by a light string of length \(l\). The bob is given a horizontal velocity \(v_0\) as shown in figure. If the string gets slack at some point P making an angle \( \theta \) from the horizontal, the ratio of the speed \(v\) of the bob at point P to its initial speed \(v_0\) is :

- NEET (UG) - 2025
- Pendulums
- Which of the following aqueous solutions will exhibit the highest boiling point?
- NEET (UG) - 2025
- Colligative Properties
Match List I with List II:

Choose the correct answer from the options given below:- NEET (UG) - 2025
- Solutions
- 5 moles of liquid X and 10 moles of liquid Y make a solution having a vapor pressure of 70 torr. The vapor pressures of pure X and Y are 63 torr and 78 torr, respectively. Which of the following is true regarding the described solution?
- NEET (UG) - 2025
- Solutions
Among the following, choose the ones with an equal number of atoms.
- 212 g of Na2CO3 (s) [molar mass = 106 g]
- 248 g of NaNO3 (s) [molar mass = 62 g]
- 240 g of NaOH (s) [molar mass = 40 g]
- 12 g of H2 (g) [molar mass = 2 g]
- 220 g of CO2 (g) [molar mass = 44 g]
Choose the correct answer from the options given below:
- NEET (UG) - 2025
- Stoichiometry and Stoichiometric Calculations