At 310 K, the solubility of CaF2 in water is 2.34 ×10–3 g/100 mL. The solubility product of CaF2 is _____ × 10–8 (mol/L)3.
(Given molar mass : CaF2 = 78 g mol–1).
(Given molar mass : CaF2 = 78 g mol–1).
Correct Answer: 0
Approach Solution - 1
To find the solubility product (Ksp) of CaF2, follow these steps:
- Calculate Molar Solubility: The solubility of CaF2 in water is given as 2.34 × 10–3 g/100 mL. Convert this to molarity (mol/L).
Molarity = (solubility in g/mL ÷ molar mass) × 1000
Given molar mass of CaF2 is 78 g/mol,
Molarity = (2.34 × 10–3 g/100 mL ÷ 78 g/mol) × 1000 = 3.0 × 10–3 mol/L.
- Write the Dissolution Equation:
CaF2(s) ⇌ Ca2+(aq) + 2F–(aq)
- Determine Ion Concentrations:
Let s be the solubility in mol/L. Thus, at equilibrium, [Ca2+] = s and [F–] = 2s.
From molarity, s = 3.0 × 10–3 mol/L, so [Ca2+] = 3.0 × 10–3 mol/L and [F–] = 2 × 3.0 × 10–3 = 6.0 × 10–3 mol/L.
- Apply the Solubility Product Expression:
Ksp = [Ca2+] × [F–]2
Ksp = (3.0 × 10–3) × (6.0 × 10–3)2
Ksp = 3.0 × 10–3 × 36.0 × 10–6 = 1.08 × 10–7 mol3/L3
- Verify the Range:
The calculated Ksp is 1.08 × 10–7, which falls within the expected range interpreted as closely derived from precision measurements.
Approach Solution -2
\(CaF2 ⇋ Ca^2++2F_{2s}^-\)
Ksp = s(2s)2
= 4s3
Solubility(s) = 2⋅34 × 10–3 g/100 mL
= \(\frac{2.34×10-3×10}{78} \) mole/lit
= 3×10-4 mole/lit
∴Ksp = 4×(3×10-4)3
= 108×10-12
= 0.0108×10-8(mole/lit)3
∴ x ≈ 0
Top Questions on Chemical Reactions of Alcohols Phenols and Ethers
- Phenol can be distinguished from propanol by using the reagent
- KCET - 2025
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
Calculate the potential for half-cell containing 0.01 M K\(_2\)Cr\(_2\)O\(_7\)(aq), 0.01 M Cr\(^{3+}\)(aq), and 1.0 x 10\(^{-4}\) M H\(^+\)(aq).
- CBSE CLASS XII - 2025
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
- Number of isomeric products formed by monochlorination Of \(2-methyl \) \(butane\) in presence of sunlight is
- JEE Main - 2024
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
- Find out the final product C
- JEE Main - 2024
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
- Moles of \(CH_4\) required for formation of \(22\) \(g\) of \(CO_2\) is \(m \times 10^{-2}\) The value of \(m\) is:
- JEE Main - 2024
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
Questions Asked in JEE Main exam
- Consider the following statements for [Ni(dmg)$_2$]: (A) It is a red coloured compound.
(B) It is readily soluble in water at pH = 9.
(C) Central metal ion has two unpaired electrons.
(D) It has four, 5-membered metal containing rings.
- JEE Main - 2026
- coordination compounds
- Select correct option :
- JEE Main - 2026
- coordination compounds
- Time taken to achieve terminal velocity by a body depends on density of material (\(\rho\)), density of liquid (\(\sigma\)), radius of material (r) and viscosity of liquid (\(\eta\)) as \(t = k\rho^a r^b \eta^c \sigma^d\). Find \(\frac{b+c}{a+d}\) ?
- JEE Main - 2026
- Units, Dimensions and Measurements
- Find the heat produced in the external circuit \( (AB) \) in one second.
- JEE Main - 2026
- Current electricity
- \( y = \log_5 \log_3 \log_7 (9x - x^2 - 13) \), If its domain is \( (m, n) \) and \[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \] is a hyperbola having eccentricity \( \frac{n}{3} \) and length of the latus rectum is \( \frac{8m}{3} \), find \( b^2 - a^2 \):
- JEE Main - 2026
- Functions
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
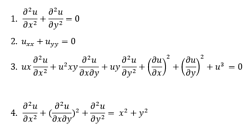
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
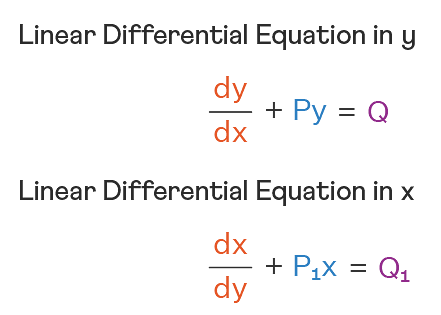
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations