A metallic rod of length ' \(L\) ' is rotated with an angular speed of ' \(\omega\) ' normal to a uniform magnetic field ' \(B\) ' about an axis passing through one end of rod as shown in figure. The induced emf will be :
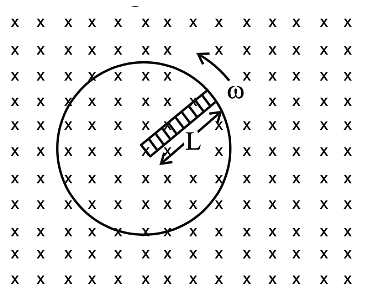
A metallic rod of length ' \(L\) ' is rotated with an angular speed of ' \(\omega\) ' normal to a uniform magnetic field ' \(B\) ' about an axis passing through one end of rod as shown in figure. The induced emf will be :
Show Hint
For a rotating rod in a uniform magnetic field, the induced EMF is given by:
\[ \epsilon = \frac{1}{2} B L^2 \omega, \]
where \( B \) is the magnetic field, \( L \) is the length of the rod, and \( \omega \) is the angular speed.
\(\frac{1}{2} B ^2 L ^2 \omega\)
\(\frac{1}{4} BL ^2 \omega\)
\(\frac{1}{2} BL ^2 \omega\)
\(\frac{1}{4} B ^2 L \omega\)
The Correct Option is C
Approach Solution - 1
When the rod rotates about one end in a uniform magnetic field, the induced EMF is calculated using Faraday’s law. The differential EMF generated across an infinitesimal length \( dx \) of the rod is:
\[ d\epsilon = Bv \, dx \]
where:
- \( v = \omega x \) is the linear velocity of the element at a distance \( x \) from the axis of rotation,
- \( B \) is the uniform magnetic field.
Substitute \( v = \omega x \):
\[ d\epsilon = B(\omega x) \, dx = B\omega x \, dx \]
The total EMF is obtained by integrating \( d\epsilon \) along the length of the rod:
\[ \epsilon = \int_0^L B\omega x \, dx \]
\[ \epsilon = B\omega \int_0^L x \, dx \]
\[ \epsilon = B\omega \left[ \frac{x^2}{2} \right]_0^L = B\omega \frac{L^2}{2} \]
Thus, the total induced EMF is:
\[ \epsilon = \frac{1}{2} BL^2 \omega \]
Approach Solution -2
The correct answer is (C) : $\frac{1}{2} BL ^2 \omega $
∫dε=∫B(ωx)dx
ε=Bω0∫Lxdx=2BωL2
Top Questions on Electromagnetic induction
- You are required to design an air-filled solenoid of inductance 0.016 H having a length 0.81 m and radius 0.02 m. The number of turns in the solenoid should be:
- CBSE CLASS XII - 2025
- Physics
- Electromagnetic induction
- A rectangular metallic loop is moving out of a uniform magnetic field region to a field-free region with a constant speed. When the loop is partially inside the magnetic field, the plot of the magnitude of the induced emf \( (\varepsilon) \) with time \( (t) \) is given by: \includegraphics[width=1\linewidth]{3.png}
- JEE Main - 2025
- Physics
- Electromagnetic induction
- A conducting bar moves on two conducting rails as shown in the figure. A constant magnetic field \( B \) exists into the page. The bar starts to move from the vertex at time \( t = 0 \) with a constant velocity. If the induced EMF is \( E \propto t^n \), then the value of \( n \) is ________________________.

- JEE Main - 2025
- Physics
- Electromagnetic induction
- Consider two long co-axial solenoids \( S_1 \) and \( S_2 \), each of length \( l \) (\( l \gg r_2 \)) and radius \( r_1 \) and \( r_2 \) (\( r_2>r_1 \)). The number of turns per unit length are \( n_1 \) and \( n_2 \), respectively. Derive an expression for mutual inductance \( M_{12} \) of solenoid \( S_1 \) with respect to solenoid \( S_2 \). Show that \( M_{21} = M_{12} \).
- CBSE CLASS XII - 2025
- Physics
- Electromagnetic induction
- The ratio of the number of turns of the primary to the secondary coils in an ideal transformer is 20:1. If 240 V AC is applied from a source to the primary coil of the transformer and a 6.0 \( \Omega \) resistor is connected across the output terminals, then the current drawn by the transformer from the source will be:
- CBSE CLASS XII - 2025
- Physics
- Electromagnetic induction
Questions Asked in JEE Main exam
- Bag 1 contains 4 white balls and 5 black balls, and Bag 2 contains n white balls and 3 black balls. One ball is drawn randomly from Bag 1 and transferred to Bag 2. A ball is then drawn randomly from Bag 2. If the probability that the ball drawn is white is \(\frac{29}{45}\), then n is equal to:
- JEE Main - 2025
- Probability
- The ratio of the magnetic field at the center of a circular coil to the magnetic field at a distance \( x \) from the center of the circular coil is:
- JEE Main - 2025
- Electromagnetism
- A cubic block of mass $ m $ is sliding down on an inclined plane at $ 60^\circ $ with an acceleration of $ \frac{g}{2} $, the value of coefficient of kinetic friction is:
- JEE Main - 2025
- Friction
- A particle is executing simple harmonic motion with a time period of 2 s and amplitude 1 cm. If \( D \) and \( d \) are the total distance and displacement covered by the particle in 12.5 s, then the ratio \( \frac{D}{d} \) is:
- JEE Main - 2025
- simple harmonic motion
- Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): Knowing initial position \( x_0 \), and initial momentum \( p_0 \) is enough to determine the position and momentum at any time \( t \) for a simple harmonic motion with a given angular frequency \( \omega \).
Reason (R): The amplitude and phase can be expressed in terms of \( x_0 \) and \( p_0 \).
In the light of the above statements, choose the correct answer from the options given below:- JEE Main - 2025
- simple harmonic motion
Concepts Used:
Electromagnetic Induction
Electromagnetic Induction is a current produced by the voltage production due to a changing magnetic field. This happens in one of the two conditions:-
- When we place the conductor in a changing magnetic field.
- When the conductor constantly moves in a stationary field.
Formula:
The electromagnetic induction is mathematically represented as:-
e=N × d∅.dt
Where
- e = induced voltage
- N = number of turns in the coil
- Φ = Magnetic flux (This is the amount of magnetic field present on the surface)
- t = time
Applications of Electromagnetic Induction
- Electromagnetic induction in AC generator
- Electrical Transformers
- Magnetic Flow Meter