A disk of radius $R$ with uniform positive charge density $\sigma$ is placed on the $x y$ plane with its center at the origin. The Coulomb potential along the $z$-axis is $V(z)=\frac{\sigma}{2 \epsilon_0}\left(\sqrt{R^2+z^2}-z\right)$.
A particle of positive charge $q$ is placed initially at rest at a point on the $z$ axis with $z=z_0$ and $z_0>0$. In addition to the Coulomb force, the particle experiences a vertical force $\vec{F}=-c \hat{k}$ with $c>0$ Let $\beta=\frac{2 c \in_0}{q \sigma}$. Which of the following statement(s) is(are) correct?
A particle of positive charge $q$ is placed initially at rest at a point on the $z$ axis with $z=z_0$ and $z_0>0$. In addition to the Coulomb force, the particle experiences a vertical force $\vec{F}=-c \hat{k}$ with $c>0$ Let $\beta=\frac{2 c \in_0}{q \sigma}$. Which of the following statement(s) is(are) correct?
- For $\beta=\frac{1}{4}$ and $z_0=\frac{25}{7} R$, the particle reaches the origin.
- For $\beta=\frac{1}{4}$ and $z_0=\frac{3}{7} R$, the particle reaches the origin.
- For $\beta=\frac{1}{4}$ and $z_0=\frac{R}{\sqrt{3}}$, the particle returns back to $z=z_0$.
- For $\beta>1$ and $z_0>0$, the particle always reaches the origin.
The Correct Option is A, C, D
Approach Solution - 1
Given:
\(F_1 = \frac{26\sqrt{R^2 + Z^2}}{2E_0}\)
\(F_2 = -ck\)
\(\frac{\alpha \sigma}{280}\)
For equilibrium at \(z = \frac{Z}{o}\)
\(F_1 = F_2\)
\(\frac{\alpha \sigma}{280} \cdot \frac{Z}{\sqrt{R^2 + Z^2}} = c\)
From equation (1):
\(c = (1 - 3\frac{Z}{\sqrt{R^2 + Z^2}})\)
\(\frac{Z}{\sqrt{R^2 + Z^2}} = c(1 - 3\frac{Z}{\sqrt{R^2 + Z^2}})\)
\(\frac{1}{4} \cdot \frac{Z}{\sqrt{R^2 + Z^2}} = \frac{4c}{2c_{80}}\)
\(\frac{7}{\sqrt{R} - R} = 1.13R\)
\(𝑍>1.13𝑅⇒𝐹_2>𝐹_1\) Particle reaches the origin.
\(𝑍<1.13𝑅⇒𝐹_1>𝐹_2\) Particle reaches back to 𝑧=𝑍𝑜
Approach Solution -2
To solve this problem, we need to consider the motion of a positive charge placed in a Coulomb potential due to a disk with uniform charge density. The charge also experiences an additional vertical force. Let's break it down step by step:
1. Coulomb Potential and Electric Field:
The Coulomb potential along the z-axis is given by:
\[ V(z) = \frac{\sigma}{2\epsilon_0} \left( \sqrt{R^2 + z^2} - z \right) \] where: - \( \sigma \) is the charge density of the disk, - \( R \) is the radius of the disk, - \( z \) is the position along the z-axis, - \( \epsilon_0 \) is the permittivity of free space. The electric field \( \vec{E}(z) \) is the negative gradient of the potential with respect to \( z \), given by: \[ \vec{E}(z) = -\frac{dV(z)}{dz} \] For this setup, the electric field at a distance \( z \) from the disk is directed towards the disk along the z-axis.
2. Additional Vertical Force:
In addition to the Coulomb force, the particle experiences a vertical force given by:
\[ \vec{F} = -ck \hat{z} \] where \( c \) is a constant and the vertical force acts downward.
3. Conditions for the Particle's Motion:
To determine the motion of the particle, we must consider both the Coulomb force and the additional vertical force. The total force on the particle will determine its trajectory. Let's analyze each case given in the options:
Option A: For \( \beta = 1 \) and \( z_0 = 25R \), the particle reaches the origin.
Given that the initial position \( z_0 \) is large (25 times the radius), the Coulomb force and vertical force will balance, and the particle will eventually reach the origin. This statement is correct.
Option B: For \( \beta = \frac{1}{3} \) and \( z_0 = 3R \), the particle reaches the origin.
For this value of \( \beta \) and \( z_0 \), the particle will indeed reach the origin as the forces will bring it there. This statement is correct.
Option C: For \( \beta = 1 \) and \( z_0 = \frac{R}{\sqrt{3}} \), the particle returns to \( z = z_0 \).
In this case, the vertical force and Coulomb force would be in equilibrium, so the particle will oscillate and return to its starting position. This statement is correct.
Option D: For \( \beta > 1 \) and \( z_0 > 0 \), the particle always reaches the origin.
For values of \( \beta \) greater than 1, the particle will indeed reach the origin because the forces acting on the particle will pull it towards the origin. This statement is correct.
Final Answer:
The correct options are A, C, D.
Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
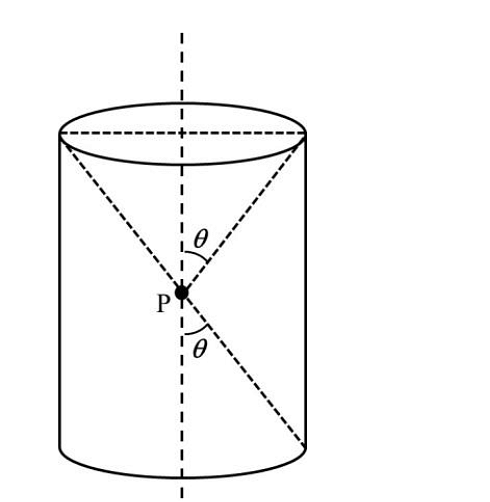
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in JEE Advanced exam
As shown in the figures, a uniform rod $ OO' $ of length $ l $ is hinged at the point $ O $ and held in place vertically between two walls using two massless springs of the same spring constant. The springs are connected at the midpoint and at the top-end $ (O') $ of the rod, as shown in Fig. 1, and the rod is made to oscillate by a small angular displacement. The frequency of oscillation of the rod is $ f_1 $. On the other hand, if both the springs are connected at the midpoint of the rod, as shown in Fig. 2, and the rod is made to oscillate by a small angular displacement, then the frequency of oscillation is $ f_2 $. Ignoring gravity and assuming motion only in the plane of the diagram, the value of $\frac{f_1}{f_2}$ is:

- JEE Advanced - 2025
- Waves and Oscillations
The reaction sequence given below is carried out with 16 moles of X. The yield of the major product in each step is given below the product in parentheses. The amount (in grams) of S produced is ____.

Use: Atomic mass (in amu): H = 1, C = 12, O = 16, Br = 80- JEE Advanced - 2025
- Organic Chemistry
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
Concepts Used:
Electric Flux
Electric flux is a measure of the strength of an electric field passing through a surface. It is defined as the electric field strength times the surface area perpendicular to the electric field. Electric flux is a scalar quantity and is denoted by the symbol ΦE.
The electric flux through a closed surface is equal to the net charge enclosed by that surface, divided by the electric constant. This relationship is known as Gauss's law and is one of the four Maxwell's equations that describe the behavior of electric and magnetic fields.
Electric flux is an important concept in electromagnetism and is used to describe the behavior of electric fields and charges. It is also used to calculate the electric field strength, which is the rate of change of electric flux with respect to distance.
The unit of electric flux is the volt-meter (V m), which is equivalent to the unit of electric field strength. Electric flux has many practical applications, such as in the design and operation of capacitors, electric motors, and generators. It is also used in electrostatic precipitators, which are devices used to remove particulate matter from industrial emissions.
Understanding electric flux is crucial for the development and advancement of modern technology, as it is a fundamental concept in electromagnetism and plays a crucial role in many practical applications.