Five charges +q, +5q, –2q, +3q and –4q are situated as shown in the figure. The electric flux due to this configuration through the surface S is
- \( \frac{5q}{\epsilon_0} \)
- \( \frac{4q}{\epsilon_0} \)
- \( \frac{3q}{\epsilon_0} \)
- \( \frac{q}{\epsilon_0} \)
The Correct Option is B
Solution and Explanation
According to Gauss’s law, the electric flux Φ through a closed surface is given by:
\(Φ = \frac{q_{in}}{\epsilon_0}\),
where qin is the total charge enclosed by the surface.
In this problem, the charges enclosed by the surface are \(q_{in} = q + (-2q) + 5q = 4q\).
Thus, the electric flux is:
\(Φ = \frac{4q}{\epsilon_0}\).
The correct answer is Option (2).
Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)
- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?
- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
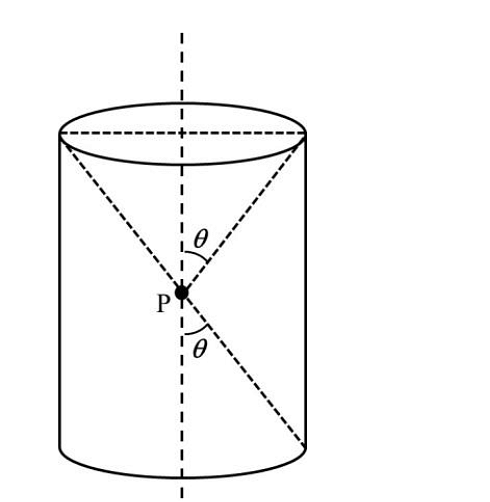
- A charge is kept at the central point \( P \) of a cylindrical region. The two edges subtend a half-angle \(\theta\) at \( P \), as shown in the figure. When \(\theta = 30^\circ\), then the electric flux through the curved surface of the cylinder is \(\Phi\). If \(\theta = 60^\circ\), then the electric flux through the curved surface becomes \(\frac{\Phi}{\sqrt{n}}\), where the value of \(n\) is \_\_\_\_. \includegraphics[width=0.3\linewidth]{ph8.png}
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in JEE Main exam
Let \[ I(x) = \int \frac{dx}{(x-11)^{\frac{11}{13}} (x+15)^{\frac{15}{13}}} \] If \[ I(37) - I(24) = \frac{1}{4} \left( b^{\frac{1}{13}} - c^{\frac{1}{13}} \right) \] where \( b, c \in \mathbb{N} \), then \[ 3(b + c) \] is equal to:
- JEE Main - 2025
- Integration
- Given below are two statements: Statement I: One mole of propyne reacts with excess of sodium to liberate half a mole of H₂ gas. Statement II: Four g of propyne reacts with NaNH₂ to liberate NH₃ gas which occupies 224 mL at STP. In the light of the above statements, choose the most appropriate answer from the options given below:
- JEE Main - 2025
- Organic Chemistry
- Given below are two statements about X-ray spectra of elements:
Statement (I):A plot of \(\sqrt {v}\) (v=frequency of X-rays emitted) vs atomic mass is a straight line.
Statement (II): A plot of v (v=frequency of X-rays emitted)} vs atomic number is a straight line.- JEE Main - 2025
- X-ray Spectra and Moseley's Law
For the thermal decomposition of \( N_2O_5(g) \) at constant volume, the following table can be formed, for the reaction mentioned below: \[ 2 N_2O_5(g) \rightarrow 2 N_2O_4(g) + O_2(g) \] Given: Rate constant for the reaction is \( 4.606 \times 10^{-2} \text{ s}^{-1} \).
- JEE Main - 2025
- Organic Chemistry
- The ratio of the power of a light source \( S_1 \) to that of the light source \( S_2 \) is 2. \( S_1 \) is emitting \( 2 \times 10^{15} \) photons per second at 600 nm. If the wavelength of the source \( S_2 \) is 300 nm, then the number of photons per second emitted by \( S_2 \) is \_\_\_\_\_ \( \times 10^{14} \).
- JEE Main - 2025
- Units and measurement