The value of \(\int_{0}^{\frac{1}{2}}\frac{dx}{\sqrt{1-x^{2n}}}\) is (n∈N)
- less than or equal to \(\frac{\pi}{6}\)
- greater than or equal to 1
- less than \(\frac{1}{2}\)
- greater than \(\frac{\pi}{6}\)
The Correct Option is B
Solution and Explanation
To solve the integral: \[ \int_0^{1/2} \left( \frac{1}{\sqrt{1 - x^2}} \right)^n dx \] Note that: \[ \frac{1}{\sqrt{1 - x^2}} = \frac{d}{dx} \arcsin x \] But since the integrand is raised to the power n, we cannot directly integrate unless n = 1. Let's analyze: \[ \left( \frac{1}{\sqrt{1 - x^2}} \right)^n = ( \arcsin' x )^n \] This is increasing on the interval \([0, 1/2]\), and for \(x \in [0, 1/2]\), \(\frac{1}{\sqrt{1 - x^2}} \geq 1\). So: \[ \left( \frac{1}{\sqrt{1 - x^2}} \right)^n \geq 1^n = 1 \] Hence: \[ \int_0^{1/2} \left( \frac{1}{\sqrt{1 - x^2}} \right)^n dx \geq \int_0^{1/2} 1 \, dx = \frac{1}{2} \] But even more tightly, since the integrand is always greater than or equal to 1 on \([0, 1/2]\), and increases as x approaches 1/2, the integral value is always: \[ \int_0^{1/2} \left( \frac{1}{\sqrt{1 - x^2}} \right)^n dx \geq 1 \] Therefore, the correct answer is: Option (B): greater than or equal to 1
Top Questions on Some Properties of Definite Integrals
- Evaluate the integral: \[ \int_{\alpha}^{\beta} \varphi(x) \, dx + \int_{\beta}^{\alpha} \varphi(x) \, dx \]
- Bihar Board XII - 2025
- Mathematics
- Some Properties of Definite Integrals
Match List-I with List-II
List-I (Definite integral) List-II (Value) (A) \( \int_{0}^{1} \frac{2x}{1+x^2}\, dx \) (I) 2 (B) \( \int_{-1}^{1} \sin^3x \cos^4x\, dx \) (II) \(\log_e\!\left(\tfrac{3}{2}\right)\) (C) \( \int_{0}^{\pi} \sin x\, dx \) (III) \(\log_e 2\) (D) \( \int_{2}^{3} \frac{2}{x^2 - 1}\, dx \) (IV) 0
Choose the correct answer from the options given below:- CUET (UG) - 2025
- Mathematics
- Some Properties of Definite Integrals
- $\int_{\pi/6}^{\pi/3} \frac{\tan x}{\tan x + \cot x} dx$ is equal to
- CUET (UG) - 2025
- Mathematics
- Some Properties of Definite Integrals
- $\int_{1}^{4} |x - 2| dx$ is equal to
- CUET (UG) - 2025
- Mathematics
- Some Properties of Definite Integrals
Match List-I with List-II
List-I (Definite integral) List-II (Value) (A) \( \int_{0}^{1} \frac{2x}{1+x^2}\, dx \) (I) 2 (B) \( \int_{-1}^{1} \sin^3x \cos^4x\, dx \) (II) \(\log_e\!\left(\tfrac{3}{2}\right)\) (C) \( \int_{0}^{\pi} \sin x\, dx \) (III) \(\log_e 2\) (D) \( \int_{2}^{3} \frac{2}{x^2 - 1}\, dx \) (IV) 0
Choose the correct answer from the options given below:- CUET (UG) - 2025
- Mathematics
- Some Properties of Definite Integrals
Questions Asked in WBJEE exam
- The variation of displacement with time of a simple harmonic motion (SHM) for a particle of mass \( m \) is represented by: \[ y = 2 \sin \left( \frac{\pi}{2} + \phi \right) \, \text{cm} \] The maximum acceleration of the particle is:
- WBJEE - 2025
- simple harmonic motion
- Ruma reached the metro station and found that the escalator was not working. She walked up the stationary escalator with velocity \( v_1 \) in time \( t_1 \). On another day, if she remains stationary on the escalator moving with velocity \( v_2 \), the escalator takes her up in time \( t_2 \). The time taken by her to walk up with velocity \( v_1 \) on the moving escalator will be:
- WBJEE - 2025
- Relative Motion
- A force \( \mathbf{F} = ai + bj + ck \) is acting on a body of mass \( m \). The body was initially at rest at the origin. The co-ordinates of the body after time \( t \) will be:
- WBJEE - 2025
- Newtons Laws of Motion
A quantity \( X \) is given by: \[ X = \frac{\epsilon_0 L \Delta V}{\Delta t} \] where:
- \( \epsilon_0 \) is the permittivity of free space,
- \( L \) is the length,
- \( \Delta V \) is the potential difference,
- \( \Delta t \) is the time interval.
The dimension of \( X \) is the same as that of:- WBJEE - 2025
- Dimensional Analysis
- Which logic gate is represented by the following combination of logic gates?

- WBJEE - 2025
- Logic gates
Concepts Used:
Definite Integral
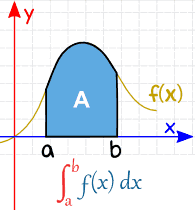
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below: