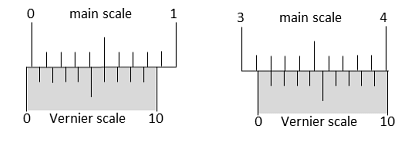
The smallest division on the main scale of a Vernier calipers is $01 \,cm$ Ten divisions of the Vernier scale correspond to nine divisions of the main scale The figure below on the left shows the reading of this calipers with no gap between its two jaws The figure on the right shows the reading with a solid sphere held between the jaws The correct diameter of the sphere is

- 3.07 cm
- 3.11 cm
- 3.15 cm
- 3.17 cm
The Correct Option is C
Solution and Explanation
Step 1: Identify the least count (L.C) of the Vernier calipers
The least count is the smallest measurement that can be accurately read using the instrument. It is given as:
L.C = 0.01 cm
This means the Vernier calipers can measure up to one-hundredth of a centimeter accurately.
Step 2: Account for the systematic error
Sometimes, the instrument may have a zero error or a systematic error due to misalignment or calibration issues. In this case, it is given that there is an error equivalent to 4 least counts:
Error = 4 × L.C = 4 × 0.01 cm = 0.04 cm
This error needs to be added to the observed measurement to obtain the true value.
Step 3: Determine the observed reading
The observed measurement from the Vernier calipers consists of two parts:
- Main scale reading = 3.1 cm
- Vernier scale reading = 1 division = 1 × 0.01 cm = 0.01 cm
So, Observed reading = 3.1 cm + 0.01 cm = 3.11 cm
Step 4: Add the error to get the corrected value
To get the correct diameter of the sphere, the error is added to the observed value:
Corrected diameter = 3.11 cm + 0.04 cm = 3.15 cm
Final Answer:
Therefore, the correct diameter of the sphere is 3.15 cm
Correct option: Option (C)
Top Questions on Units and measurement
Match the LIST-I with LIST-II
LIST-I LIST-II A. Boltzmann constant I. \( \text{ML}^2\text{T}^{-1} \) B. Coefficient of viscosity II. \( \text{MLT}^{-3}\text{K}^{-1} \) C. Planck's constant III. \( \text{ML}^2\text{T}^{-2}\text{K}^{-1} \) D. Thermal conductivity IV. \( \text{ML}^{-1}\text{T}^{-1} \) Choose the correct answer from the options given below :
- JEE Main - 2025
- Physics
- Units and measurement
- A person measures mass of 3 different particles as 435.42 g, 226.3 g and 0.125 g. According to the rules for arithmetic operations with significant figures, the additions of the masses of 3 particles will be.
- JEE Main - 2025
- Physics
- Units and measurement
- What are the units of viscosity, intensity of wave, and pressure gradient?
- JEE Main - 2025
- Chemistry
- Units and measurement
- Choose the correct statements:
(A) Weight of a substance is the amount of matter present in it.
(B) Mass is the force exerted by gravity on an object.
(C) Volume is the amount of space occupied by a substance.
(D) Temperatures below 0°C are possible in Celsius scale, but in Kelvin scale negative temperature is not possible.
(E) Precision refers to the closeness of various measurements for the same quantity. Choose the correct answer from the options given below:- JEE Main - 2025
- Chemistry
- Units and measurement
The ratio of the power of a light source \( S_1 \) to that of the light source \( S_2 \) is 2. \( S_1 \) is emitting \( 2 \times 10^{15} \) photons per second at 600 nm. If the wavelength of the source \( S_2 \) is 300 nm, then the number of photons per second emitted by \( S_2 \) is ________________ \( \times 10^{14} \).
- JEE Main - 2025
- Physics
- Units and measurement
Questions Asked in JEE Advanced exam
Let $ y(x) $ be the solution of the differential equation $$ x^2 \frac{dy}{dx} + xy = x^2 + y^2, \quad x > \frac{1}{e}, $$ satisfying $ y(1) = 0 $. Then the value of $ 2 \cdot \frac{(y(e))^2}{y(e^2)} $ is ________.
- JEE Advanced - 2025
- Differential equations
- The correct order of the wavelength maxima of the absorption band in the ultraviolet-visible region for the given complexes is:
- JEE Advanced - 2025
- coordination compounds
- Calculate the sum of magnetic moments (in Bohr Magnetons, B.M.) of the complexes: \[ [\mathrm{MnCl}_6]^{3-} \quad \text{and} \quad [\mathrm{Mn(CN)}_6]^{3-} \]
- JEE Advanced - 2025
- coordination compounds
- Consider the depicted hydrogen (H) in the hydrocarbons given below. The most acidic hydrogen (H) is:
- JEE Advanced - 2025
- Acids and Bases
- Consider a star of mass $ m_2 $ kg revolving in a circular orbit around another star of mass $ m_1 $ kg with $ m_1 \gg m_2 $. The heavier star slowly acquires mass from the lighter star at a constant rate of $ \gamma $ kg/s. In this transfer process, there is no other loss of mass. If the separation between the centers of the stars is $ r $, then its relative rate of change $ \frac{1}{r} \frac{dr}{dt} $ (in s$^{-1}$) is given by:
- JEE Advanced - 2025
- Gravitation
Concepts Used:
Units and Measurement
Unit:
A unit of a physical quantity is an arbitrarily chosen standard that is broadly acknowledged by the society and in terms of which other quantities of similar nature may be measured.
Measurement:
The process of measurement is basically a comparison process. To measure a physical quantity, we have to find out how many times a standard amount of that physical quantity is present in the quantity being measured. The number thus obtained is known as the magnitude and the standard chosen is called the unit of the physical quantity.
Read More: Fundamental and Derived Units of Measurement
System of Units:
- CGS system
- FPS system
- MKS system
- SI units
Types of Units:
Fundamental Units -
The units defined for the fundamental quantities are called fundamental units.
Derived Units -
The units of all other physical quantities which are derived from the fundamental units are called the derived units.