Question:
The minimum wavelength of X-rays produced by 20 keV electrons is nearly
The minimum wavelength of X-rays produced by 20 keV electrons is nearly
Show Hint
The minimum wavelength of X-rays decreases as the energy of the incident electrons increases, following the inverse relationship $\lambda_{\text{min}} \propto \frac{1}{E}$.
Updated On: Jun 4, 2025
- 0.62 \AA
- 1.8 \AA
- 3.2 \AA
- 6.5 \AA
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Let’s break this down step by step to calculate the minimum wavelength of X-rays produced by 20 keV electrons and determine why option (1) is the correct answer.
Step 1: Understand the concept of minimum wavelength of X-rays
The minimum wavelength ($\lambda_{\text{min}}$) of X-rays produced by electrons occurs when all the kinetic energy of the electron is converted into the energy of the X-ray photon. This is given by:
\[ E = \frac{hc}{\lambda_{\text{min}}} \]
A practical formula in electron volts and angstroms is:
\[ \lambda_{\text{min}} (\text{in \AA}) = \frac{12398}{E (\text{in eV})} \]
where $hc \approx 12398 \, \text{eV \AA}$.
Step 2: Identify the given values and calculate the wavelength
This is approximately 0.62 \AA.
Step 3: Confirm the correct answer
The calculated minimum wavelength is 0.62 \AA, which matches option (1). The term “nearly” in the question accounts for slight rounding.
Thus, the correct answer is (1) 0.62 \AA.
Step 1: Understand the concept of minimum wavelength of X-rays
The minimum wavelength ($\lambda_{\text{min}}$) of X-rays produced by electrons occurs when all the kinetic energy of the electron is converted into the energy of the X-ray photon. This is given by:
\[ E = \frac{hc}{\lambda_{\text{min}}} \]
A practical formula in electron volts and angstroms is:
\[ \lambda_{\text{min}} (\text{in \AA}) = \frac{12398}{E (\text{in eV})} \]
where $hc \approx 12398 \, \text{eV \AA}$.
Step 2: Identify the given values and calculate the wavelength
- Energy of electrons, $E = 20 \, \text{keV} = 20 \times 10^3 \, \text{eV} = 20000 \, \text{eV}$
This is approximately 0.62 \AA.
Step 3: Confirm the correct answer
The calculated minimum wavelength is 0.62 \AA, which matches option (1). The term “nearly” in the question accounts for slight rounding.
Thus, the correct answer is (1) 0.62 \AA.
Was this answer helpful?
0
0
Top Questions on X Rays and the Ordering of the Elements
- The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
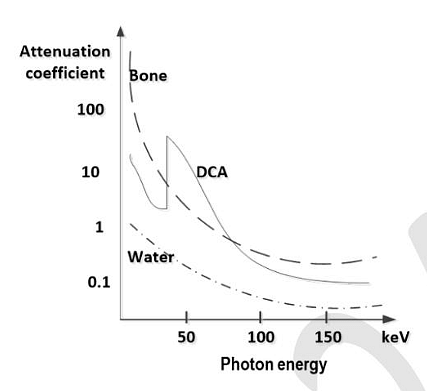
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- Which one of the following events is NOT typically encountered in diagnostic X-ray projection radiography ?
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
View More Questions
Questions Asked in AP EAPCET exam
- In a series LCR circuit, the voltages across the capacitor, resistor, and inductor are in the ratio 2:3:6. If the voltage of the source in the circuit is 240 V, then the voltage across the inductor is
- AP EAPCET - 2025
- Electromagnetic induction
- 0.25 moles of $ \text{CH}_2\text{FCOOH} $ was dissolved in $ 0.5 \, \text{kg} $ of water. The depression in freezing point of the resultant solution was observed as $ 1^\circ \text{C} $. What is the van't Hoff factor? ($ K_f = 1.86 \, \text{K kg mol}^{-1} $)
- AP EAPCET - 2025
- Colligative Properties
- At $T(K)$, the vapor pressure of water is $x$ kPa. What is the vapor pressure (in kPa) of 1 molal solution containing non-volatile solute?
- AP EAPCET - 2025
- Colligative Properties
- At 300 K, vapour pressure of pure liquid A is 70 mm Hg. It forms an ideal solution with liquid B. Mole fraction of B = 0.2 and total vapour pressure of solution = 84 mm Hg. What is vapour pressure (in mm) of pure B?
- AP EAPCET - 2025
- Colligative Properties
- A 1% (w/v) aqueous solution of a certain solute is isotonic with a 3% (w/v) solution of glucose (molar mass 180 g mol$^{-1}$). The molar mass of solute (in g mol$^{-1}$) is
- AP EAPCET - 2025
- Colligative Properties
View More Questions