Question:
In the x-ray reflection (n=1), the distance between two parallel planes of NaCl is 280 pm and diffraction angle is 5.2°. What is the wavelength of its light radiation?
In the x-ray reflection (n=1), the distance between two parallel planes of NaCl is 280 pm and diffraction angle is 5.2°. What is the wavelength of its light radiation?
Show Hint
For X-ray diffraction, use Bragg's law to relate the wavelength to the angle of diffraction.
Updated On: May 15, 2025
- 0.504 \(\text{Å}\)
- 5.04 \(\text{Å}\)
- 50.4 \(\text{Å}\)
- 504 \(\text{Å}\)
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
We can use Bragg's law for diffraction to find the wavelength of the X-ray:
\[
n\lambda = 2d \sin(\theta)
\]
where:
- \(n = 1\) (diffraction order)
- \(\lambda\) is the wavelength
- \(d = 280 \, \text{pm} = 280 \times 10^{-12} \, \text{m}\)
- \(\theta = 5.2^\circ\)
Now, substituting the known values:
\[
\lambda = \frac{2 \times 280 \times 10^{-12} \times \sin(5.2^\circ)}{1}
\]
\[
\lambda = 0.504 \, \text{Å}
\]
Thus, the correct answer is \( \boxed{0.504 \, \text{Å}} \).
Was this answer helpful?
0
0
Top Questions on X Rays and the Ordering of the Elements
- In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The minimum wavelength of X-rays produced by 20 keV electrons is nearly
- AP EAPCET - 2025
- Physics
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
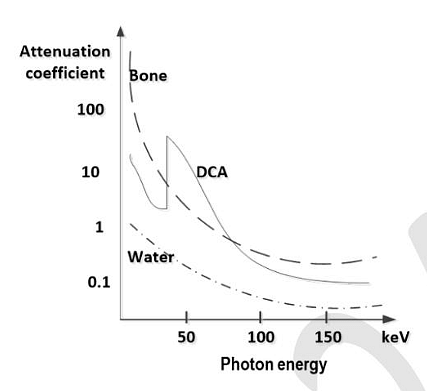
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
View More Questions
Questions Asked in AP EAPCET exam
- If $$ \int \frac{dx}{1 - \sin^4 x} = A \tan x + B \tan^{-1}(\sqrt{2} \tan x) + C, $$ then find $ A^2 - B^2 $.
- AP EAPCET - 2025
- Integration
- In compound (X), hyperconjugation is present and in (Y), resonance effect is present. What are X and Y, respectively?
- AP EAPCET - 2025
- Organic Chemistry
- A family consists of 8 persons. If 4 persons are chosen at random and they are found to be 2 men and 2 women, then the probability that there are equal numbers of men and women in that family is:
- AP EAPCET - 2025
- Probability
- The total maximum number of electrons possible in 3d, 6d, 5s and 4f orbitals with \(m_l\) (magnetic quantum number) value -2 is
- AP EAPCET - 2025
- Atomic Structure
- If \[ A = \begin{bmatrix} 1 & -1 & 2 \\ -2 & 3 & -3 \\ 4 & -4 & 5 \end{bmatrix} \] and \( A^T \) represents the transpose of \( A \), then calculate \( AA^T - A - A^T \).
- AP EAPCET - 2025
- Matrices
View More Questions