Question:
The equation of motion of system is given by . The damped vibration, can be written as:
The equation of motion of system is given by . The damped vibration, can be written as:
Updated On: Aug 9, 2023
- (A)
- (B)
- (C) Both A and B
(D) Neither A nor B
Hide Solution
Verified By Collegedunia
The Correct Option is C
Approach Solution - 1
Explanation:
The general case of damped harmonic motion:Where the stiffness of spring, damping coefficient and massDamped vibration of a system is defined as:(1)Damping ratio : It is defined as the ratio of actual damping to the critical damping.Substitute the value of in equation 1, we get,Hence the correct option is (C).
The general case of damped harmonic motion:Where the stiffness of spring, damping coefficient and massDamped vibration of a system is defined as:(1)Damping ratio : It is defined as the ratio of actual damping to the critical damping.Substitute the value of in equation 1, we get,Hence the correct option is (C).
Was this answer helpful?
0
0
Hide Solution
Verified By Collegedunia
Approach Solution -2
The oscillation in which the amplitude decreases gradually with time is called damped oscillation.
- The decrease in amplitude is due to air drag and friction.
- A damped oscillator is approximately periodic with decreasing amplitude.
Equation of Damped Oscillation
The equation of damped oscillation is given by
\[m\frac{d^2\,x}{dt^2\,x}+b\frac{dx\,}{dt\,}+kx=0\]Where
- m is the mass
- k is restoring force constant or spring constant
- b is a positive constant depends on the characteristic of the medium and size and shape of the block etc.
The solution of the above equation is given by
\(x(t)=Ae\frac{bt\,}{2m\,}cos\)
Where
- A’ = Ae(-bt/2m) represents the amplitude of the damped oscillation.
- ω’ = angular frequency of the damped oscillation.
The angular frequency of the damped oscillation can be represented by
w'=√(k/m-b^2/4m^2)
Was this answer helpful?
0
0
Learn with videos:
Top Questions on Force and Laws of Motion
- A particle of mass \( m \) is under the influence of the gravitational field of a body of mass \( M \) (\( M \gg m \)). The particle is moving in a circular orbit of radius \( r_0 \) with time period \( T_0 \) around the mass \( M \). Then, the particle is subjected to an additional central force, corresponding to the potential energy \( V(r) = \frac{\alpha m{r^3} \), where \( \alpha \) is a positive constant of suitable dimensions and r is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius \(r_0\) in the combined gravitational potential due to M and \(V_c(r)\), but with a new time period \(T_1\), then } \[ \frac{T_1^2 - T_0^2}{T_1^2} \] is given by: [G is the gravitational constant]
- JEE Advanced - 2024
- Physics
- Force and Laws of Motion
- A car travelling at a speed of 30 km/h is brought to halt in 8m by applying brakes. If the same car is traveling at 60 km/h, in how many meters can it be brought to halt with the same braking? (Provide answer in m)
- NATA - 2023
- Physics
- Force and Laws of Motion
- The child has to choose which of the following horses A, B, C or D if he has to experience faster revolution
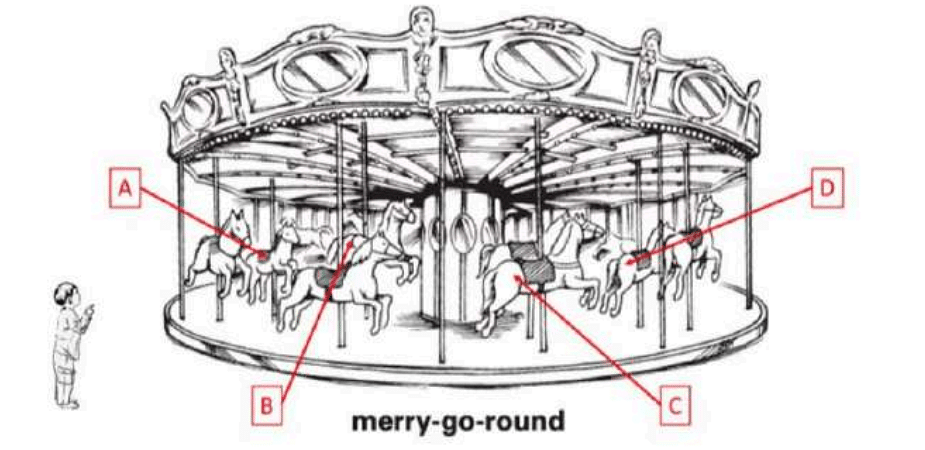
- NATA - 2023
- Physics
- Force and Laws of Motion
- A Girl Starts her Motion in a straight line at a Velocity of 60 m/s, her Velocity is Changing at a Constant Rate. If She Stops after 60 s, what is her Acceleration?
- NATA - 2023
- Physics
- Force and Laws of Motion
- Which of the men from X, Y, Z will fall faster to the ground when they are jumping from an airplane, ignoring the air resistance.
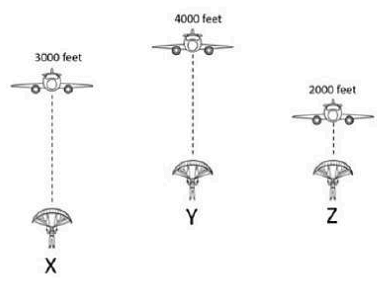
- NATA - 2023
- Physics
- Force and Laws of Motion
View More Questions
Questions Asked in JEE Main exam

In the first configuration (1) as shown in the figure, four identical charges \( q_0 \) are kept at the corners A, B, C and D of square of side length \( a \). In the second configuration (2), the same charges are shifted to mid points C, E, H, and F of the square. If \( K = \frac{1}{4\pi \epsilon_0} \), the difference between the potential energies of configuration (2) and (1) is given by:
- JEE Main - 2025
- Electromagnetic Field (EMF)
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- Ice at \( -5^\circ C \) is heated to become vapor with temperature of \( 110^\circ C \) at atmospheric pressure. The entropy change associated with this process can be obtained from:
- JEE Main - 2025
- Thermodynamics
- Let C be the circle of minimum area enclosing the ellipse E: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \) with eccentricity \( \frac{1}{2} \) and foci \( (\pm 2, 0) \). Let PQR be a variable triangle, whose vertex P is on the circle C and the side QR of length 29 is parallel to the major axis and contains the point of intersection of E with the negative y-axis. Then the maximum area of the triangle PQR is:
- JEE Main - 2025
- Coordinate Geometry
- Let circle $C$ be the image of
$$ x^2 + y^2 - 2x + 4y - 4 = 0 $$
in the line
$$ 2x - 3y + 5 = 0 $$
and $A$ be the point on $C$ such that $OA$ is parallel to the x-axis and $A$ lies on the right-hand side of the centre $O$ of $C$.
If $B(\alpha, \beta)$, with $\beta < 4$, lies on $C$ such that the length of the arc $AB$ is $\frac{1}{6}$ of the perimeter of $C$, then $\beta - \sqrt{3}\alpha$ is equal to:
View More Questions
