Question:
A particle of mass \( m \) is under the influence of the gravitational field of a body of mass \( M \) (\( M \gg m \)). The particle is moving in a circular orbit of radius \( r_0 \) with time period \( T_0 \) around the mass \( M \). Then, the particle is subjected to an additional central force, corresponding to the potential energy \( V(r) = \frac{\alpha m{r^3} \), where \( \alpha \) is a positive constant of suitable dimensions and r is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius \(r_0\) in the combined gravitational potential due to M and \(V_c(r)\), but with a new time period \(T_1\), then }
\[
\frac{T_1^2 - T_0^2}{T_1^2}
\]
is given by: [G is the gravitational constant]
A particle of mass \( m \) is under the influence of the gravitational field of a body of mass \( M \) (\( M \gg m \)). The particle is moving in a circular orbit of radius \( r_0 \) with time period \( T_0 \) around the mass \( M \). Then, the particle is subjected to an additional central force, corresponding to the potential energy \( V(r) = \frac{\alpha m{r^3} \), where \( \alpha \) is a positive constant of suitable dimensions and r is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius \(r_0\) in the combined gravitational potential due to M and \(V_c(r)\), but with a new time period \(T_1\), then }
\[
\frac{T_1^2 - T_0^2}{T_1^2}
\]
is given by: [G is the gravitational constant]
Show Hint
Analyze forces and potentials to find the net effect on orbital time periods.
Updated On: Jan 20, 2025
- \( \frac{3\alpha}{GMr_0^2} \)
- \( \frac{\alpha}{2GMr_0^2} \)
- \( \frac{\alpha}{GMr_0^2} \)
- \( \frac{2\alpha}{GMr_0^2} \)
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
The additional force is:
\[
F = -\frac{dV}{dr} = -\frac{3\alpha m}{r^4}.
\]
The net centripetal force is:
\[
F_{\text{net}} = \frac{GMm}{r_0^2} + \frac{3\alpha m}{r_0^4}.
\]
The time period is:
\begin{align*}
T_1 &= \frac{2\pi t_0}{v} = \sqrt{\frac{2\pi t_0^2}{Gmr_0^3 - 3\alpha}}
\text{Also,} \quad T_0^2 &= \frac{4\pi^2 r_0^3}{Gm}
\frac{T_1^2 - T_0^2}{T_1^2} &= -1 - \frac{T_0^2}{T_1^2} = -1 - \frac{4\pi^2 r_0^3}{Gm} \frac{Gmr_0^3 - 3\alpha}{2\pi t_0^2 r_0^3}
&= 1 - 1 + \frac{3\alpha}{Gmr_0 t_0^2} } \end{align*} Expanding: \[ = \frac{3\alpha}{GMr_0^2} \]
\text{Also,} \quad T_0^2 &= \frac{4\pi^2 r_0^3}{Gm}
\frac{T_1^2 - T_0^2}{T_1^2} &= -1 - \frac{T_0^2}{T_1^2} = -1 - \frac{4\pi^2 r_0^3}{Gm} \frac{Gmr_0^3 - 3\alpha}{2\pi t_0^2 r_0^3}
&= 1 - 1 + \frac{3\alpha}{Gmr_0 t_0^2} } \end{align*} Expanding: \[ = \frac{3\alpha}{GMr_0^2} \]
Was this answer helpful?
0
0
Top Questions on Force and Laws of Motion
- A car travelling at a speed of 30 km/h is brought to halt in 8m by applying brakes. If the same car is traveling at 60 km/h, in how many meters can it be brought to halt with the same braking? (Provide answer in m)
- NATA - 2023
- Physics
- Force and Laws of Motion
- The child has to choose which of the following horses A, B, C or D if he has to experience faster revolution
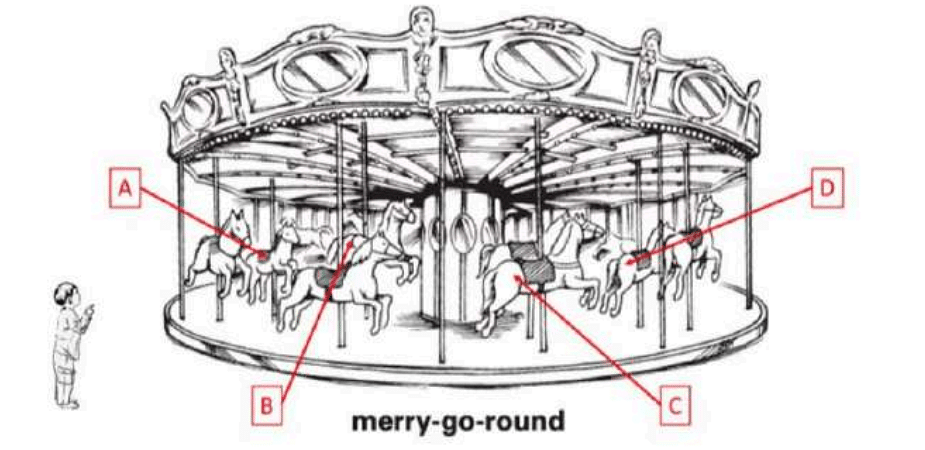
- NATA - 2023
- Physics
- Force and Laws of Motion
- A Girl Starts her Motion in a straight line at a Velocity of 60 m/s, her Velocity is Changing at a Constant Rate. If She Stops after 60 s, what is her Acceleration?
- NATA - 2023
- Physics
- Force and Laws of Motion
- Which of the men from X, Y, Z will fall faster to the ground when they are jumping from an airplane, ignoring the air resistance.
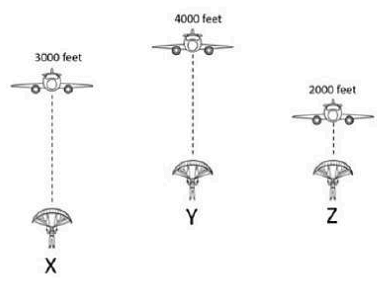
- NATA - 2023
- Physics
- Force and Laws of Motion
- The concept of displacement current was introduced by___.
- NATA - 2023
- Physics
- Force and Laws of Motion
View More Questions
Questions Asked in JEE Advanced exam
- Let $ x_0 $ be the real number such that $ e^{x_0} + x_0 = 0 $. For a given real number $ \alpha $, define $$ g(x) = \frac{3xe^x + 3x - \alpha e^x - \alpha x}{3(e^x + 1)} $$ for all real numbers $ x $. Then which one of the following statements is TRUE?
- JEE Advanced - 2025
- Fundamental Theorem of Calculus
- A linear octasaccharide (molar mass = 1024 g mol$^{-1}$) on complete hydrolysis produces three monosaccharides: ribose, 2-deoxyribose and glucose. The amount of 2-deoxyribose formed is 58.26 % (w/w) of the total amount of the monosaccharides produced in the hydrolyzed products. The number of ribose unit(s) present in one molecule of octasaccharide is _____.
Use: Molar mass (in g mol$^{-1}$): ribose = 150, 2-deoxyribose = 134, glucose = 180; Atomic mass (in amu): H = 1, O = 16- JEE Advanced - 2025
- Biomolecules
Let $ P(x_1, y_1) $ and $ Q(x_2, y_2) $ be two distinct points on the ellipse $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$ such that $ y_1 > 0 $, and $ y_2 > 0 $. Let $ C $ denote the circle $ x^2 + y^2 = 9 $, and $ M $ be the point $ (3, 0) $. Suppose the line $ x = x_1 $ intersects $ C $ at $ R $, and the line $ x = x_2 $ intersects $ C $ at $ S $, such that the $ y $-coordinates of $ R $ and $ S $ are positive. Let $ \angle ROM = \frac{\pi}{6} $ and $ \angle SOM = \frac{\pi}{3} $, where $ O $ denotes the origin $ (0, 0) $. Let $ |XY| $ denote the length of the line segment $ XY $. Then which of the following statements is (are) TRUE?
- JEE Advanced - 2025
- Conic sections
- Adsorption of phenol from its aqueous solution on to fly ash obeys Freundlich isotherm. At a given temperature, from 10 mg g$^{-1}$ and 16 mg g$^{-1}$ aqueous phenol solutions, the concentrations of adsorbed phenol are measured to be 4 mg g$^{-1}$ and 10 mg g$^{-1}$, respectively. At this temperature, the concentration (in mg g$^{-1}$) of adsorbed phenol from 20 mg g$^{-1}$ aqueous solution of phenol will be ____. Use: $\log_{10} 2 = 0.3$
- JEE Advanced - 2025
- Adsorption
- At 300 K, an ideal dilute solution of a macromolecule exerts osmotic pressure that is expressed in terms of the height (h) of the solution (density = 1.00 g cm$^{-3}$) where h is equal to 2.00 cm. If the concentration of the dilute solution of the macromolecule is 2.00 g dm$^{-3}$, the molar mass of the macromolecule is calculated to be $X \times 10^{4}$ g mol$^{-1}$. The value of $X$ is ____. Use: Universal gas constant (R) = 8.3 J K$^{-1}$ mol$^{-1}$ and acceleration due to gravity (g) = 10 m s$^{-2}\}$
- JEE Advanced - 2025
- Colligative Properties
View More Questions