Question:
The child has to choose which of the following horses A, B, C or D if he has to experience faster revolution
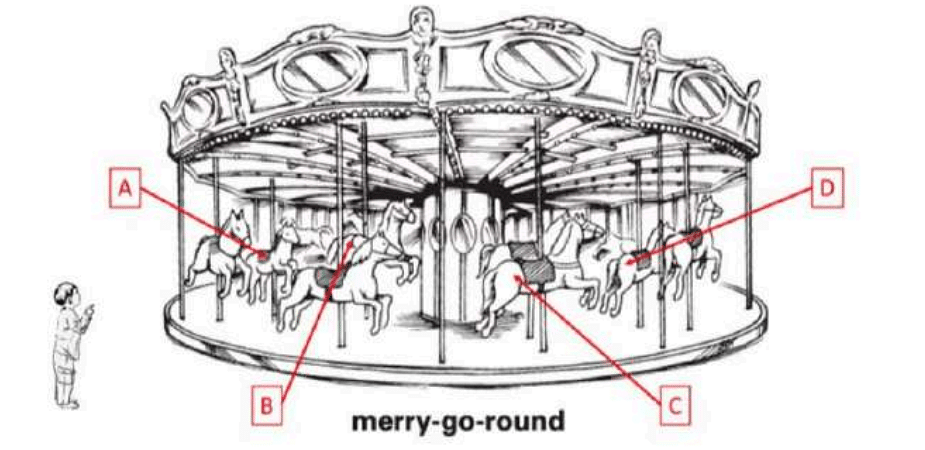
The child has to choose which of the following horses A, B, C or D if he has to experience faster revolution
Updated On: Jun 25, 2024
Hide Solution
Verified By Collegedunia
Solution and Explanation
The correct Answer is C
Was this answer helpful?
0
0
Top Questions on Force and Laws of Motion
- A particle of mass \( m \) is under the influence of the gravitational field of a body of mass \( M \) (\( M \gg m \)). The particle is moving in a circular orbit of radius \( r_0 \) with time period \( T_0 \) around the mass \( M \). Then, the particle is subjected to an additional central force, corresponding to the potential energy \( V(r) = \frac{\alpha m{r^3} \), where \( \alpha \) is a positive constant of suitable dimensions and r is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius \(r_0\) in the combined gravitational potential due to M and \(V_c(r)\), but with a new time period \(T_1\), then } \[ \frac{T_1^2 - T_0^2}{T_1^2} \] is given by: [G is the gravitational constant]
- JEE Advanced - 2024
- Physics
- Force and Laws of Motion
- A car travelling at a speed of 30 km/h is brought to halt in 8m by applying brakes. If the same car is traveling at 60 km/h, in how many meters can it be brought to halt with the same braking? (Provide answer in m)
- NATA - 2023
- Physics
- Force and Laws of Motion
- A Girl Starts her Motion in a straight line at a Velocity of 60 m/s, her Velocity is Changing at a Constant Rate. If She Stops after 60 s, what is her Acceleration?
- NATA - 2023
- Physics
- Force and Laws of Motion
- Which of the men from X, Y, Z will fall faster to the ground when they are jumping from an airplane, ignoring the air resistance.
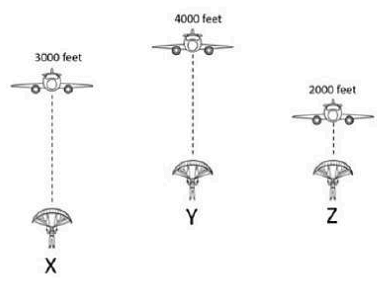
- NATA - 2023
- Physics
- Force and Laws of Motion
- The concept of displacement current was introduced by___.
- NATA - 2023
- Physics
- Force and Laws of Motion
View More Questions
Questions Asked in NATA exam
- A boy gave a bundle of RS.100 notes to a guy. The serial number of notes are from CJJ103440 to CJJ103490. What is the total amount given to the guy
- NATA - 2024
- General Aptitude
- Mirror image of a clock shows 8:50. What will the actual time?
- NATA - 2024
- General Aptitude
- Find the next number in the series 5, 20, 24, 6, 2, 8,
- NATA - 2024
- General Aptitude
- What is another word for 'LOFT'?
- NATA - 2024
- Architectural Knowledge
- Identify the building material:
- NATA - 2024
- Architectural Knowledge
View More Questions