Question:
Let
\[
S = \{(x, y) \in \mathbb{R} \times \mathbb{R} : x \geq 0, y \geq 0, y^2 \leq 4x, y^2 \leq 12 - 2x, \text{ and } 3y + \sqrt{8}x \leq 5\sqrt{8}\}.
\]
If the area of the region \( S \) is \( \alpha \sqrt{2} \), then \( \alpha \) is equal to:
Let
\[
S = \{(x, y) \in \mathbb{R} \times \mathbb{R} : x \geq 0, y \geq 0, y^2 \leq 4x, y^2 \leq 12 - 2x, \text{ and } 3y + \sqrt{8}x \leq 5\sqrt{8}\}.
\]
If the area of the region \( S \) is \( \alpha \sqrt{2} \), then \( \alpha \) is equal to:
Show Hint
When solving geometry problems involving inequalities, sketch the region to visualize limits of integration.
Updated On: Jan 20, 2025
- \( \frac{17}{2} \)
- \( \frac{17}{3} \)
- \( \frac{17}{4} \)
- \( \frac{17}{5} \)
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
To find the area of the region \( S \), we compute the integral:
\[
\text{Required Area} = \int_0^2 \sqrt{x} \, dx + 1 \cdot 3 \cdot \sqrt{8}.
\]
Evaluating step by step:
\begin{align*}
y^2 &= 4x, y^2 = 12 - 2x \Rightarrow x = 2, y = \sqrt{8}
A &= \int_{0}^{2} 2\sqrt{x} \, dx + \frac{1}{2} \times 3 \times \sqrt{8}
&= \left[2 \times \frac{2}{3}x^{\frac{3}{2}}\right]_{0}^{2} + 3\sqrt{2} = \frac{4}{3} \times 2\sqrt{2} + 3\sqrt{2} = \frac{17}{3}\sqrt{2}
\therefore \end{align*} Adding the remaining area: \[ \text{Total Area} = \alpha\sqrt{2} \Rightarrow \alpha = \frac{17}{3} \] Thus, \( \alpha = \frac{17}{3} \).
A &= \int_{0}^{2} 2\sqrt{x} \, dx + \frac{1}{2} \times 3 \times \sqrt{8}
&= \left[2 \times \frac{2}{3}x^{\frac{3}{2}}\right]_{0}^{2} + 3\sqrt{2} = \frac{4}{3} \times 2\sqrt{2} + 3\sqrt{2} = \frac{17}{3}\sqrt{2}
\therefore \end{align*} Adding the remaining area: \[ \text{Total Area} = \alpha\sqrt{2} \Rightarrow \alpha = \frac{17}{3} \] Thus, \( \alpha = \frac{17}{3} \).
Was this answer helpful?
0
0
Top Questions on Area Of A Parallelogram
- The area of the parallelogram, whose adjacent sides are given by the vectors \(\vec{a} = 2\hat{i} - \hat{j} + 5\hat{k}\) and \(\vec{b} = 2\hat{i} + \hat{j} + 2\hat{k}\), is:
- CUET (UG) - 2024
- Mathematics
- Area Of A Parallelogram
- Let \( \overrightarrow{OA} = \vec{a}, \overrightarrow{OB} = 12\vec{a} + 4\vec{b} \) and \( \overrightarrow{OC} = \vec{b} \), where \( O \) is the origin. If \( S \) is the parallelogram with adjacent sides \( OA \) and \( OC \), then\[\frac{\text{area of the quadrilateral OABC}}{\text{area of } S}\]is equal to ___.
- JEE Main - 2024
- Mathematics
- Area Of A Parallelogram
- Considering only the principal values of the inverse trigonometric functions, the value of \[ \tan\left( \sin^{-1}\left(\frac{3}{5}\right) - 2 \cos^{-1}\left(\frac{2}{\sqrt{5}}\right) \right) \] is:
- JEE Advanced - 2024
- Mathematics
- Area Of A Parallelogram
- If the lengths of the diagonals of a rhombus are 24 cm and 10 cm, then each side of the rhombus is
- AP POLYCET - 2023
- Mathematics
- Area Of A Parallelogram
- If four vertices of a parallelogram are (-3,-1),(a,b),(3,3) and (4,3) taken in order,then the ratio of a and b is
- AP POLYCET - 2023
- Mathematics
- Area Of A Parallelogram
View More Questions
Questions Asked in JEE Advanced exam
- A charge is kept at the central point \( P \) of a cylindrical region. The two edges subtend a half-angle \(\theta\) at \( P \), as shown in the figure. When \(\theta = 30^\circ\), then the electric flux through the curved surface of the cylinder is \(\Phi\). If \(\theta = 60^\circ\), then the electric flux through the curved surface becomes \(\frac{\Phi}{\sqrt{n}}\), where the value of \(n\) is \_\_\_\_. \includegraphics[width=0.3\linewidth]{ph8.png}
- JEE Advanced - 2024
- Electric Flux
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
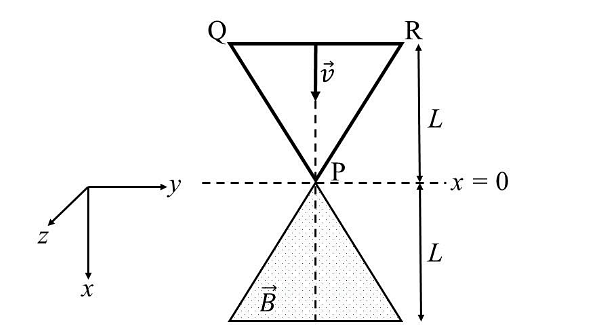
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - A positive, singly ionized atom of mass number \(A_M\) is accelerated from rest by the voltage \(192 V\). Thereafter, it enters a rectangular region of width 𝑤 with magnetic field \(\bar{B_0} = 0.1𝑘̂\)Tesla, as shown in the figure. The ion finally hits a detector at the distance 𝑥 below its starting trajectory. [Given: Mass of neutron/proton =\((5/3) × 10^{−27}\) kg, charge of the electron \(= 1.6 × 10^{−19} C.\)]
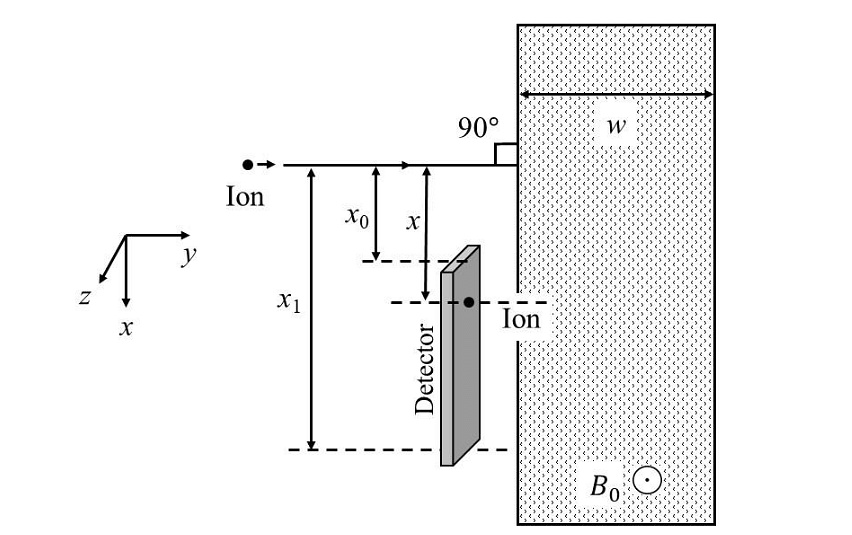
Which of the following option(s) is(are) correct?- JEE Advanced - 2024
- Electromagnetic waves
- Among the following, the correct statement(s) for electrons in an atom is(are)
- JEE Advanced - 2024
- Structure of atom
- An organic compound \(P\) with molecular formula \(C_6H_6O_3\) gives a ferric chloride test and does not have an intramolecular hydrogen bond. The compound \(P\) reacts with 3 equivalents of \(NH_2OH\) to produce oxime \(Q\). Treatment of \(P\) with excess methyl iodide in the presence of \(KOH\) produces compound \(R\) as the major product. Reaction of \(R\) with excess iso-butylmagnesium bromide followed by treatment with \(H_3O^+\) gives compound \(S\) as the major product. The total number of methyl (\(-CH_3\)) groups in compound \(S\) is \_\_\_\_\_.
- JEE Advanced - 2024
- Qualitative Analysis
View More Questions