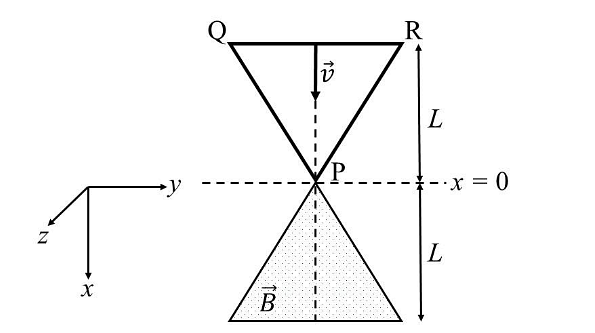
A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?

Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0?
The Correct Option is A
Approach Solution - 1
To solve the problem, we need to analyze the variation of the induced emf in a conducting triangular loop moving through a region of uniform magnetic field.
1. Understanding the Setup:
- The loop PQR is an equilateral triangle of height \( L \) moving along the \( +x \)-direction.
- The magnetic field \( \vec{B} \) is uniform and points in the \( +z \)-direction.
- At \( x=0 \), vertex P enters the magnetic field region.
- The induced emf \( E \) is related to the rate of change of magnetic flux through the loop.
2. Variation of Flux and emf:
- Initially, no part of the loop is inside the magnetic field, so \( E = 0 \).
- As the loop enters the field (from \( x=0 \) to \( x=L \)), the area inside the field increases linearly, so flux increases linearly.
- The emf \( E = -d\Phi/dt \) is proportional to the rate of change of flux.
- When half the loop enters (\( x=L/2 \)), the rate of change of area changes slope.
- Between \( x=L \) and \( x=2L \), the loop is leaving the field and the flux decreases.
- Beyond \( x=2L \), the loop is completely outside, so \( E = 0 \).
3. Shape of emf vs. distance graph:
- The emf starts at zero at \( x=0 \), decreases (negative slope) until \( x=L/2 \), then increases until \( x=L \).
- After \( x=L \), emf is zero until \( x=3L/2 \), then increases positively until \( x=2L \), and finally returns to zero.
- This corresponds to graph (A) with negative and positive triangular peaks.
Final Answer:
Option (A)
Approach Solution -2
To solve the problem, analyze how the induced emf in the loop changes as the loop moves through the magnetic field region.
1. Setup:
- The loop PQR is an equilateral triangle of height \(L\), moving along the +x direction.
- Magnetic field \(\vec{B}\) is uniform and directed along +z.
- Induced emf \(E\) is related to the rate of change of magnetic flux through the loop.
- At \(x=0\), vertex P enters the magnetic field region.
2. Flux and emf behavior:
- For \(0 \leq x < L\): increasing part of the loop enters the field.
- The flux increases non-linearly, first faster then slower due to triangular shape.
- This results in a changing induced emf with negative and positive slopes at different points.
- For \(L \leq x \leq 2L\): the loop leaves the magnetic field region.
- The flux decreases similarly, giving a characteristic emf pattern.
3. Graph Interpretation:
- The induced emf first decreases (negative peak) as the loop enters.
- Then it increases to zero at \(x=L\).
- After that, it stays zero for some region.
- Finally, it increases positively as the loop leaves the field and goes back to zero at \(x=2L\).
- This matches graph (A).
Final Answer:
Option (A)
Top Questions on torque
- An electric dipole of dipole moment \( 1.0 \times 10^{-12} \ \text{Cm} \) lies along the x-axis. An electric field of magnitude \( 2.0 \times 10^4 \ \text{NC}^{-1} \) is switched on at an instant in the region. The unit vector along the electric field is \( \frac{\sqrt{3}}{2} \hat{i} + \frac{1}{2} \hat{j} \). The magnitude of the torque acting on the dipole at that instant is:
- A cube having a side of 10 cm with unknown mass and 200 gm mass were hung at two ends of an uniform rigid rod of 27 cm long. The rod along with masses was placed on a wedge keeping the distance between wedge point and 200 gm weight as 25 cm. Initially the masses were not at balance. A beaker is placed beneath the unknown mass and water is added slowly to it. At given point the masses were in balance and half volume of the unknown mass was inside the water. (Take the density of the unknown mass is more than that of the water, the mass did not absorb water and water density is 1 gm/cm$^3$.) The unknown mass is ______ kg.
- The coordinates of a particle with respect to origin in a given reference frame is \( (1, 1, 1) \) meters. If a force of \( \mathbf{F} = \hat{i} - \hat{j} + \hat{k} \) acts on the particle, then the magnitude of torque (with respect to origin) in the z-direction is:
- The coordinates of a particle with respect to origin in a given reference frame is \( (1, 1, 1) \) meters. If a force of \( \mathbf{F} = \hat{i} - \hat{j} + \hat{k} \) acts on the particle, then the magnitude of torque (with respect to origin) in the z-direction is:
- A uniform rod of mass 250 g having length 100 cm is balanced on a sharp edge at the 40 cm mark. A mass of 400 g is suspended at the 10 cm mark. To maintain the balance of the rod, the mass to be suspended at the 90 cm mark is:
Questions Asked in JEE Advanced exam
- Consider a star of mass $ m_2 $ kg revolving in a circular orbit around another star of mass $ m_1 $ kg with $ m_1 \gg m_2 $. The heavier star slowly acquires mass from the lighter star at a constant rate of $ \gamma $ kg/s. In this transfer process, there is no other loss of mass. If the separation between the centers of the stars is $ r $, then its relative rate of change $ \frac{1}{r} \frac{dr}{dt} $ (in s$^{-1}$) is given by:
- JEE Advanced - 2025
- Gravitation
- A projectile is thrown at an angle of \(60^\circ\) with the horizontal. Initial speed is \(270\, \text{m/s}\). A linear drag force \(F = -CV\) acts on the body. Find the horizontal displacement till \(t = 2\) seconds. Given \(C = 0.1\, \text{s}^{-1}\).
- JEE Advanced - 2025
- Projectile motion
The reaction sequence given below is carried out with 16 moles of X. The yield of the major product in each step is given below the product in parentheses. The amount (in grams) of S produced is ____.

Use: Atomic mass (in amu): H = 1, C = 12, O = 16, Br = 80- JEE Advanced - 2025
- Organic Chemistry
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
As shown in the figures, a uniform rod $ OO' $ of length $ l $ is hinged at the point $ O $ and held in place vertically between two walls using two massless springs of the same spring constant. The springs are connected at the midpoint and at the top-end $ (O') $ of the rod, as shown in Fig. 1, and the rod is made to oscillate by a small angular displacement. The frequency of oscillation of the rod is $ f_1 $. On the other hand, if both the springs are connected at the midpoint of the rod, as shown in Fig. 2, and the rod is made to oscillate by a small angular displacement, then the frequency of oscillation is $ f_2 $. Ignoring gravity and assuming motion only in the plane of the diagram, the value of $\frac{f_1}{f_2}$ is:

- JEE Advanced - 2025
- Waves and Oscillations



