Let $f: R \rightarrow R$ be defined as,
$f(x) =
\begin{cases}
-55x, & \text{if } x < -5 \\
2x^3 -3x^2 -120x, & \text{if } 5 \le x \le 4 \\
2x^3 -3x^2-36x-336& \text{if } x > 4,
\end{cases} $
Let $A=\{ x \in R : f$ is increasing $\} .$ Then $A$ is equal to
- $(-\infty,-5) \cup(4, \infty)$
- $(-5, \infty)$
- $(-\infty,-5) \cup(-4, \infty)$
- (-5,-4)$\cup(4, \infty)$
The Correct Option is D
Approach Solution - 1
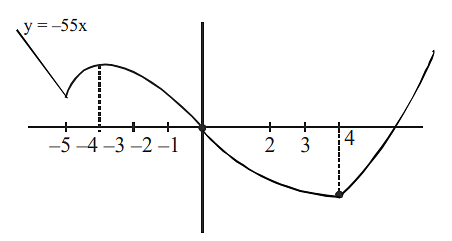
Approach Solution -2
The correct answer is (D) : (-5,-4)\(\cup(4, \infty)\)
For f'(x) ≥ 0
Case I :- -5 < x < 4
Then f'(x) ≥ 0 ≥ 0 implies
6x2 - 6x - 120 ≥ 0
⇒ x2 - x - 20 ≥ 0
⇒ (x - 5) (x + 4) ≥ 0
⇒ x ≤ - 4 or x ≥ 5
But -5 <x <4
∴ -5 < x < 4
Hence, function f(x) increases in domain x ∈ (-5, -4)
Case II :- x > 4
Then f'(x) ≥ ≥ 0 implies
6x2 - 6x - 36 ≥ 0
⇒ x2 - x - 6 ≥ 0
⇒ (x - 3) (x + 2) ≥ 0
⇒ x ≤ - 2 or x ≥ 3
But x > 4
Hence, f(x) increases in (4, ∞ )
From both cases, we can say that f(x) is increases in (-5, -4) U (4, ∞ ).
A = {x|x ∈ (-5, -4) U (4, ∞ )}
Top Questions on Functions
- In \( I(m, n) = \int_0^1 x^{m-1} (1-x)^{n-1} \, dx \), where \( m, n > 0 \), then \( I(9, 14) + I(10, 13) \) is:
- The sum of all local minimum values of the function \( f(x) \) as defined below is:
\[ f(x) = \begin{cases} 1 - 2x & \text{if } x < -1, \\[10pt] \frac{1}{3}(7 + 2|x|) & \text{if } -1 \leq x \leq 2, \\[10pt] \frac{11}{18}(x-4)(x-5) & \text{if } x > 2. \end{cases} \] If the domain of the function \( f(x) = \dfrac{1}{\sqrt{10 + 3x - x^2}} + \dfrac{1}{\sqrt{x + |x|}} \) is \( (a, b) \), then \((1 + a)^2 + b^2\) is equal to:
- The area of the region enclosed by the curves \( y = e^x \), \( y = |e^x - 1| \), and the y-axis is:
- The integral \[ 80 \int_0^{\frac{\pi}{4}} \frac{(\sin \theta + \cos \theta)}{(9 + 16 \sin 2\theta)} \, d\theta \] is equal to:
Questions Asked in JEE Main exam
- Two balls are selected at random one by one without replacement from a bag containing 4 white and 6 black balls. If the probability that the first selected ball is black, given that the second selected ball is also black, is \(\frac{m}{n}\), where gcd(m, n) = 1, then m + n is equal to:
- JEE Main - 2025
- Probability
- A tiny metallic rectangular sheet has length and breadth of 5 mm and 2.5 mm, respectively. Using a specially designed screw gauge which has pitch of 0.75 mm and 15 divisions in the circular scale, you are asked to find the area of the sheet. In this measurement, the maximum fractional error will be \( \frac{x}{100} \), where \( x \) is:
- JEE Main - 2025
- Units and measurement
- The sum of the series $ 2 \times 1 \times 20C_4 - 3 \times 2 \times 20C_5 + 4 \times 3 \times 20C_6 - 5 \times 4 \times 20C_7 + ... + 18 \times 17 \times 20C_{20}, \text{is equal to} $
- JEE Main - 2025
- Algebra
- Let \( A = \{1, 2, 3, 4\} \) and \( B = \{1, 4, 9, 16\} \). Then the number of many-one functions \( f: A \to B \) such that \( 1 \in f(A) \) is equal to:
- JEE Main - 2025
- Counting functions
- Let $ A = \{-3, -2, -1, 0, 1, 2, 3\} $ and $ R $ be a relation on $ A $ defined by $ xRy $ if and only if $ 2x - y \in \{0, 1\} $. Let $ l $ be the number of elements in $ R $. Let $ m $ and $ n $ be the minimum number of elements required to be added in $ R $ to make it reflexive and symmetric relations, respectively. Then $ l + m + n $ is equal to:
- JEE Main - 2025
- Relations
Concepts Used:
Functions
A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets, mapping from A to B will be a function only when every element in set A has one end only one image in set B.
Kinds of Functions
The different types of functions are -
One to One Function: When elements of set A have a separate component of set B, we can determine that it is a one-to-one function. Besides, you can also call it injective.
Many to One Function: As the name suggests, here more than two elements in set A are mapped with one element in set B.
Moreover, if it happens that all the elements in set B have pre-images in set A, it is called an onto function or surjective function.
Also, if a function is both one-to-one and onto function, it is known as a bijective. This means, that all the elements of A are mapped with separate elements in B, and A holds a pre-image of elements of B.
Read More: Relations and Functions