Question:
Let \( f : \mathbb{R} \to \mathbb{R} \) be a function defined by
\[
f(x) =
\begin{cases}
x^2 \sin\left(\frac{\pi}{x^2}\right), & \text{if } x \neq 0, \\
0, & \text{if } x = 0.
\end{cases}
\]
Then which of the following statements is TRUE?
Let \( f : \mathbb{R} \to \mathbb{R} \) be a function defined by
\[
f(x) =
\begin{cases}
x^2 \sin\left(\frac{\pi}{x^2}\right), & \text{if } x \neq 0, \\
0, & \text{if } x = 0.
\end{cases}
\]
Then which of the following statements is TRUE?
Show Hint
To solve trigonometric equations, express the argument in terms of known solutions, like \( n\pi \) for \(\sin(x) = 0\), and analyze the constraints on \( n \) based on the interval.
Updated On: Jan 20, 2025
- \( f(x) = 0 \) has infinitely many solutions in the interval \( \left[\frac{1}{10^{10}}, \infty\right). \)
- \( f(x) = 0 \) has no solutions in the interval \( \left[\frac{1}{\pi}, \infty\right). \)
- The set of solutions of \( f(x) = 0 \) is in the interval \( \left(0, \frac{1}{10^{10}}\right]. \)
- \( f(x) = 0 \) has more than 25 solutions in the interval \( \left(\frac{1}{\pi^2}, \frac{1}{\pi}\right]. \)
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
We are given:
\[
x^2 \sin\left(\frac{\pi}{x^2}\right) = 0.
\]
This implies:
\[
\sin\left(\frac{\pi}{x^2}\right) = 0 \quad \text{(for \( x \neq 0 \))}.
\]
This is satisfied when:
\[
\frac{\pi}{x^2} = n\pi, \quad \text{so } x = \frac{1}{\sqrt{n}}, \quad (n>0).
\]
If \( x \in \left(\frac{1}{\pi^2}, \frac{1}{\pi}\right] \), then:
\[
\frac{1}{\pi^2}<\frac{1}{\sqrt{n}} \leq \frac{1}{\pi}.
\]
Squaring all sides:
\[
\frac{1}{\pi^4}<\frac{1}{n} \leq \frac{1}{\pi^2}.
\]
Taking reciprocals:
\[
\pi^4>n \geq \pi^2.
\]
Approximating \( \pi^4 \approx 97 \) and \( \pi^2 \approx 9 \), we find:
\[
n = 9, 10, 11, \ldots, 97.
\]
Thus, there are more than 25 solutions for \( f(x) = 0 \) in the interval \( \left(\frac{1}{\pi^2}, \frac{1}{\pi}\right]. \)
Was this answer helpful?
0
0
Top Questions on Integral Calculus
- Find the value of the integral: \[ \int_0^e \log_e x \, dx \]
- JEE Main - 2025
- Mathematics
- Integral Calculus
- For the function \( f(x) = \ln(x^2 + 1) \), what is the second derivative of \( f(x) \)?
- JEE Main - 2025
- Mathematics
- Integral Calculus
- If \[ 24 \left( \int_0^\frac{\pi}{4} \left[ \sin \left( 4x - \frac{\pi}{12} \right) + [2 \sin x] \right] dx \right) = 2n + \alpha, \] where [.] denotes the greatest integer function, then \( \alpha \) is equal to:
- JEE Main - 2025
- Mathematics
- Integral Calculus
- Find the value of the integral \( \int_0^{\frac{\pi}{2}} \sin^2(x) \, dx \).
- JEE Main - 2025
- Mathematics
- Integral Calculus
- Evaluate the integral: \[ \int \frac{x^2 - 1}{x^4 + 3x^2 + 1} \, dx \]
- KEAM - 2024
- Mathematics
- Integral Calculus
View More Questions
Questions Asked in JEE Advanced exam
- A region in the form of an equilateral triangle (in x-y plane) of height L has a uniform magnetic field 𝐵⃗ pointing in the +z-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height 𝐿, is placed in the x-y plane with its vertex P at x = 0 in the orientation shown in the figure. At 𝑡 = 0, the loop starts entering the region of the magnetic field with a uniform velocity 𝑣 along the +x-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
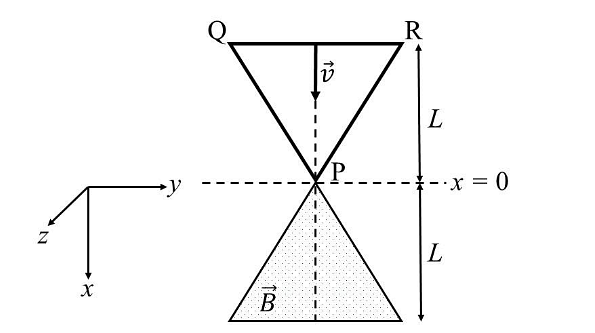
Which of the following graph best depicts the variation of the induced emf (E) in the loop as a function of the distance (𝑥) starting from 𝑥 = 0? - A positive, singly ionized atom of mass number \(A_M\) is accelerated from rest by the voltage \(192 V\). Thereafter, it enters a rectangular region of width 𝑤 with magnetic field \(\bar{B_0} = 0.1𝑘̂\)Tesla, as shown in the figure. The ion finally hits a detector at the distance 𝑥 below its starting trajectory. [Given: Mass of neutron/proton =\((5/3) × 10^{−27}\) kg, charge of the electron \(= 1.6 × 10^{−19} C.\)]

Which of the following option(s) is(are) correct?- JEE Advanced - 2024
- Electromagnetic waves
- Among the following, the correct statement(s) for electrons in an atom is(are)
- JEE Advanced - 2024
- Structure of atom
- An organic compound \(P\) with molecular formula \(C_6H_6O_3\) gives a ferric chloride test and does not have an intramolecular hydrogen bond. The compound \(P\) reacts with 3 equivalents of \(NH_2OH\) to produce oxime \(Q\). Treatment of \(P\) with excess methyl iodide in the presence of \(KOH\) produces compound \(R\) as the major product. Reaction of \(R\) with excess iso-butylmagnesium bromide followed by treatment with \(H_3O^+\) gives compound \(S\) as the major product. The total number of methyl (\(-CH_3\)) groups in compound \(S\) is \_\_\_\_\_.
- JEE Advanced - 2024
- Qualitative Analysis
- An organic compound P having molecular formula C6H6O3 gives ferric chloride test and does not have intramolecular hydrogen bond. The compound P reacts with 3 equivalents of NH2OH to produce oxime Q. Treatment of P with excess methyl iodide in the presence of KOH produces compound R as the major product. Reaction of R with excess iso-butylmagnesium bromide followed by treatment with H3O+ gives compound S as the major product.
The total number of methyl (−CH3) group(s) in compound S is ____.- JEE Advanced - 2024
- Aldehydes, Ketones and Carboxylic Acids
View More Questions