Let
\(a→=α\^{i}+3\^{j}−\^{k}, \overrightarrow{b}=3\^{i}−β\^{j}+4\^{k} and \overrightarrow{c}=\^{i}+2\^{j}−2\^{k }\)
where α,β∈R, be three vectors. If the projection of
\(\overrightarrow{a} on \overrightarrow{c} is \frac{10}{3} and \overrightarrow{b}×\overrightarrow{c}=−6\^{i}+10\^{j}+7\^{k}, \)
then the value of α+β is equal to
Let
\(a→=α\^{i}+3\^{j}−\^{k}, \overrightarrow{b}=3\^{i}−β\^{j}+4\^{k} and \overrightarrow{c}=\^{i}+2\^{j}−2\^{k }\)
where α,β∈R, be three vectors. If the projection of
\(\overrightarrow{a} on \overrightarrow{c} is \frac{10}{3} and \overrightarrow{b}×\overrightarrow{c}=−6\^{i}+10\^{j}+7\^{k}, \)
then the value of α+β is equal to
- 3
- 4
- 5
- 6
The Correct Option is A
Solution and Explanation
The correct option is(A): 3

Top Questions on types of differential equations
- If \( m_1 \) and \( m_2 \) are the slopes of the direct common tangents drawn to the circles \[ x^2 + y^2 - 2x - 8y + 8 = 0 \quad \text{and} \quad x^2 + y^2 - 8x + 15 = 0 \] then \( m_1 + m_2 \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If \( (2,3) \) is the focus and \( x - y + 3 = 0 \) is the directrix of a parabola, then the equation of the tangent drawn at the vertex of the parabola is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If the focus of an ellipse is \((-1,-1)\), equation of its directrix corresponding to this focus is \(x + y + 1 = 0\) and its eccentricity is \(\frac{1}{\sqrt{2}}\), then the length of its major axis is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The equation of the common tangent to the parabola \(y^2 = 8x\) and the circle \(x^2 + y^2 = 2\) is \(ax + by + 2 = 0\). If \(-\frac{a}{b}>0\), then \(3a^2 + 2b + 1 =\)
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The axis of a parabola is parallel to Y-axis. If this parabola passes through the points \( (1,0), (0,2), (-1,-1) \) and its equation is \( ax^2 + bx + cy + d = 0 \), then \( \frac{ad}{bc} \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Questions Asked in JEE Main exam
- A force of 49 N acts tangentially at the highest point of a sphere (solid of mass 20 kg) kept on a rough horizontal plane. If the sphere rolls without slipping, then the acceleration of the center of the sphere is:
- JEE Main - 2025
- Quantum Mechanics
Let \( y^2 = 12x \) be the parabola and \( S \) its focus. Let \( PQ \) be a focal chord of the parabola such that \( (SP)(SQ) = \frac{147}{4} \). Let \( C \) be the circle described by taking \( PQ \) as a diameter. If the equation of the circle \( C \) is: \[ 64x^2 + 64y^2 - \alpha x - 64\sqrt{3}y = \beta, \] then \( \beta - \alpha \) is equal to:
- JEE Main - 2025
- Parabola
The expression given below shows the variation of velocity \( v \) with time \( t \): \[ v = \frac{At^2 + Bt}{C + t} \] The dimension of \( A \), \( B \), and \( C \) is:
- JEE Main - 2025
- Dimensional Analysis
The dimensions of a physical quantity \( \epsilon_0 \frac{d\Phi_E}{dt} \) are similar to [Symbols have their usual meanings]
- JEE Main - 2025
- Dimensional analysis
- Match List-I with List-II.

- JEE Main - 2025
- Dimensional analysis
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
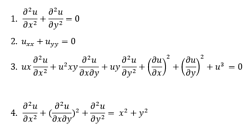
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
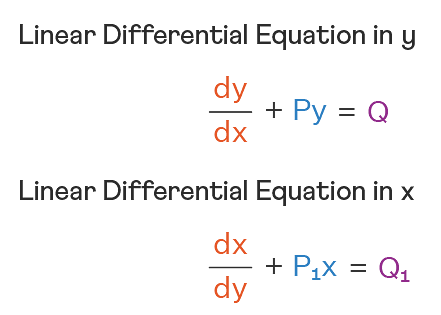
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations