In van der Wall equation
\([P=\frac{a}{V^2}[v-b]=RT;\)
P is pressure, V is volume, R is universal gas constant and T is temperature. The ratio of constants a/b is dimensionally equal to:
In van der Wall equation
\([P=\frac{a}{V^2}[v-b]=RT;\)
P is pressure, V is volume, R is universal gas constant and T is temperature. The ratio of constants a/b is dimensionally equal to:
- \(\frac{P}{V}\)
- \(\frac{V}{P}\)
- PV
- PV3
The Correct Option is C
Solution and Explanation
The correct otpion is(C): PV
From the equation
[a] ≡ [PV2] [b] ≡ [V]
\(⇒[\frac{a}{b}]≡[PV]\)
Top Questions on Ideal gas equation
- What is the ideal gas law equation?
- MHT CET - 2025
- Chemistry
- Ideal gas equation
- Which of the following gases is most likely to deviate from ideal gas behavior at high pressures and low temperatures?
- MHT CET - 2025
- Chemistry
- Ideal gas equation
- A sample of gas occupies 10 L at 300 K and 2 atm. What will be its volume at 400 K and 1 atm?
- MHT CET - 2025
- Chemistry
- Ideal gas equation
- What is the molar volume of an ideal gas at standard temperature and pressure (STP)?
- VITEEE - 2025
- Chemistry
- Ideal gas equation
- A gas occupies 2 liters at a pressure of 3 atm. What will be its volume when the pressure is reduced to 1.5 atm at constant temperature?
- AP EAPCET - 2025
- Chemistry
- Ideal gas equation
Questions Asked in JEE Main exam
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?
- JEE Main - 2026
- Organic Chemistry
- For two identical cells each having emf \(E\) and internal resistance \(r\), the current through an external resistor of \(6\,\Omega\) is the same when the cells are connected in series as well as in parallel. The value of the internal resistance \(r\) is ________ \(\Omega\).
- JEE Main - 2026
- Current electricity
- For three unit vectors \( \vec a, \vec b, \vec c \) satisfying \[ |\vec a-\vec b|^2 + |\vec b-\vec c|^2 + |\vec c-\vec a|^2 = 9 \] and \[ |2\vec a + k\vec b + k\vec c| = 3, \] the positive value of \( k \) is:
- JEE Main - 2026
- Vector Algebra
In the given figure, the blocks $A$, $B$ and $C$ weigh $4\,\text{kg}$, $6\,\text{kg}$ and $8\,\text{kg}$ respectively. The coefficient of sliding friction between any two surfaces is $0.5$. The force $\vec{F}$ required to slide the block $C$ with constant speed is ___ N.
(Given: $g = 10\,\text{m s}^{-2}$)
- JEE Main - 2026
- Rotational Mechanics
- The system of linear equations
$x + y + z = 6$
$2x + 5y + az = 36$
$x + 2y + 3z = b$
has- JEE Main - 2026
- Matrices and Determinants
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
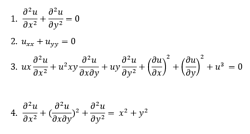
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
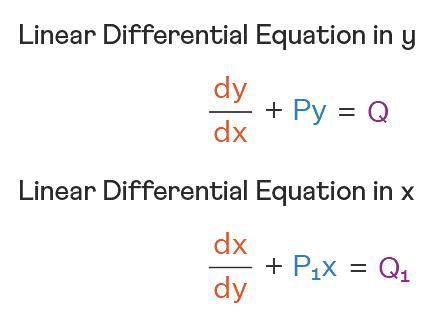
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations