In the following cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(a) (0,0,0) 3x-4y+12z=3
(b) (3,-2,1) 2x-y+2z+3=0
(c) (2,3,-5) x+2y-2z=9
(d) (-6,0,0) 2x-3y+6z-2=0
In the following cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(a) (0,0,0) 3x-4y+12z=3
(b) (3,-2,1) 2x-y+2z+3=0
(c) (2,3,-5) x+2y-2z=9
(d) (-6,0,0) 2x-3y+6z-2=0
Solution and Explanation
It is known that the distance between a point P(x1,y1,z1)and a plane Ax-+By+Cz=D, is given by,
d=\(\begin{vmatrix}\frac{AX_1+By_1+Cz_1-D}{\sqrt{A^2+B^2+C^2}} \end{vmatrix}\)|...(1)
(a) The given point is (0,0,0) and the plane is 3x-4y+12z=3
∴d=\(\begin{vmatrix}\frac{3*0-4*0+12*0-3}{\sqrt{(3)^2+(-4)^2+(12)^2}} \end{vmatrix}\)
=\(\frac{3}{\sqrt{169}}\)=\(\frac{3}{13}\)
(b)The given point is (3,-2,1) and the plane is 2x-y+2z+3=0
∴d=\(\begin{vmatrix}\frac{2*3-(-2)+2*1+3}{\sqrt{(2)^2+(-1)^2+(2)^2}} \end{vmatrix}\)
=|\(\frac{13}{3}\)| =\(\frac{13}{3}\)
(c)The given point is (2,3,-5) and the plane is x+2y-2z=9
∴d=\(\begin{vmatrix}\frac{2+2*3-2(-5)-9}{\sqrt{(1)^2+(2)^2+(-2)^2}} \end{vmatrix}\)
=\(\frac{9}{3}\)
=3
(d)The given point is (-6,0,0) and the plane is 2x-3y+6z-2=0
∴d=\(\begin{vmatrix}\frac{2(-6)-3*0+6*0-2}{\sqrt{(2)^2+(-3)^2+(6)^2}} \end{vmatrix}\)
=\(\begin{vmatrix}\frac{-14}{\sqrt{49}} \end{vmatrix}\)
=\(\frac{14}{7}\)
=2
Top Questions on Three Dimensional Geometry
- If A(2,1,-1), B(6,-3,2), C(-3,12,4) are the vertices of a triangle ABC and the equation of the plane containing the triangle ABC is $53x+by+cz+d=0$, then $\frac{d}{b+c}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If $(\alpha, \beta, \gamma)$ is the foot of the perpendicular drawn from a point $(-1,2,-1)$ to the line joining the points $(2,-1,1)$ and $(1,1,-2)$, then $\alpha+\beta+\gamma=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If m:n is the ratio in which the point $\left(\frac{8}{5}, \frac{1}{5}, \frac{8}{5}\right)$ divides the line segment joining the points (2,p,2) and (p,-2,p) where p is an integer then $\frac{3m+n}{3n}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- Let $\pi_1$ be the plane determined by the vectors $\hat{i}+\hat{j}, \hat{i}+\hat{k}$ and $\pi_2$ be the plane determined by the vectors $\hat{j}-\hat{k}, \hat{k}-\hat{i}$. Let $\vec{a}$ be a non-zero vector parallel to the line of intersection of the planes $\pi_1$ and $\pi_2$. If $\vec{b} = \hat{i}+\hat{j}-\hat{k}$ then the angle between the vectors $\vec{a}$ and $\vec{b}$ is
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
Show that the following lines intersect. Also, find their point of intersection:
Line 1: \[ \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} \]
Line 2: \[ \frac{x - 4}{5} = \frac{y - 1}{2} = z \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
Questions Asked in CBSE CLASS XII exam
- What will be formed after oxidation of secondary alcohol with chromic anhydride (CrO3)?
- CBSE CLASS XII - 2025
- Organic Reactions
- A charge \( -6 \mu C \) is placed at the center B of a semicircle of radius 5 cm, as shown in the figure. An equal and opposite charge is placed at point D at a distance of 10 cm from B. A charge \( +5 \mu C \) is moved from point ‘C’ to point ‘A’ along the circumference. Calculate the work done on the charge.

- CBSE CLASS XII - 2025
- Electrostatics
- In a region of a uniform electric field \( \mathbf{E} \), a negatively charged particle is moving with a constant velocity \( \mathbf{v} = -v_0 \hat{i} \) near a long straight conductor coinciding with XX' axis and carrying current \( I \) towards -X axis. The particle remains at a distance \( d \) from the conductor.
- CBSE CLASS XII - 2025
- Moving Charges and Magnetism
- Altima Ltd. invited applications for 2,00,000 equity shares of ₹ 10 at a premium of ₹ 4 per share. Amount payable:
On application and allotment – ₹ 7 (incl. ₹ 1 premium)
On first and final call – Balance.
Applications received for 2,40,000 shares. 30,000 rejected. Manvi allotted 4,000 shares failed to pay first and final call. Her shares were forfeited. These were reissued at ₹ 4 per share fully paid-up.
Pass journal entries in the books of Altima Ltd.- CBSE CLASS XII - 2025
- Accounting for Share Capital
- Using the mirror equation and the formula of magnification, deduce that “the virtual image produced by a convex mirror is always diminished in size and is located between the pole and the focus.”
- CBSE CLASS XII - 2025
- Mirrors and Images
Concepts Used:
Distance of a Point from a Plane
The shortest perpendicular distance from the point to the given plane is the distance between point and plane. In simple terms, the shortest distance from a point to a plane is the length of the perpendicular parallel to the normal vector dropped from the particular point to the particular plane. Let's see the formula for the distance between point and plane.
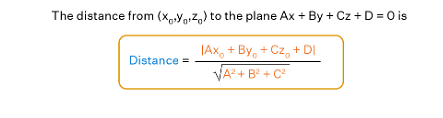
Read More: Distance Between Two Points