Question

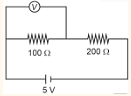
In given circuit, reading of voltmeter is 1 V, then resistance of

• A. 100 Ω
• B. 200 Ω
• C. 200√5 Ω
• D. 50 Ω

Answer 1

The Correct Option is A

The problem asks for the resistance of a voltmeter, given its reading when connected in parallel across a 100 Ω resistor in a series circuit with a 200 Ω resistor and a 5 V source.

Concept Used:

The solution utilizes the following principles of electric circuits:

1. Ohm's Law: The potential difference (voltage) \( V \) across a resistor is proportional to the current \( I \) flowing through it, given by \( V = IR \).

2. Resistors in Series: The total voltage across components in series is the sum of the individual voltages. The current is the same through all components.

3. Resistors in Parallel: The equivalent resistance \( R_p \) of two resistors \( R_a \) and \( R_b \) connected in parallel is given by:

\[ \frac{1}{R_p} = \frac{1}{R_a} + \frac{1}{R_b} \quad \text{or} \quad R_p = \frac{R_a R_b}{R_a + R_b} \]

A voltmeter has its own internal resistance and is always connected in parallel to the component across which the voltage is measured.

Step-by-Step Solution:

Step 1: Identify the given parameters from the circuit diagram.

Source voltage, \( V_s = 5 \, \text{V} \).

First resistor, \( R_1 = 100 \, \Omega \).

Second resistor, \( R_2 = 200 \, \Omega \).

Reading of the voltmeter across \( R_1 \), \( V_m = 1 \, \text{V} \).

Let the resistance of the voltmeter be \( R_V \).

Step 2: Determine the voltage across the 200 Ω resistor.

The voltmeter and the 100 Ω resistor form a parallel combination. This combination is in series with the 200 Ω resistor. The sum of the voltage across the parallel part (\( V_m \)) and the voltage across the 200 Ω resistor (\( V_{200} \)) must equal the source voltage.

\[ V_s = V_m + V_{200} \] \[ 5 \, \text{V} = 1 \, \text{V} + V_{200} \] \[ V_{200} = 5 - 1 = 4 \, \text{V} \]

Step 3: Calculate the total current flowing from the source.

This total current \( I \) flows through the 200 Ω resistor. Using Ohm's law for this resistor:

\[ I = \frac{V_{200}}{R_2} = \frac{4 \, \text{V}}{200 \, \Omega} = \frac{1}{50} \, \text{A} = 0.02 \, \text{A} \]

Step 4: Calculate the equivalent resistance of the parallel combination.

The voltmeter reading \( V_m = 1 \, \text{V} \) is the potential difference across the parallel combination of the 100 Ω resistor and the voltmeter. Let the equivalent resistance of this parallel part be \( R_p \). Using Ohm's law for this part:

\[ V_m = I \times R_p \] \[ 1 \, \text{V} = (0.02 \, \text{A}) \times R_p \] \[ R_p = \frac{1}{0.02} = 50 \, \Omega \]

Step 5: Use the equivalent parallel resistance to find the voltmeter's resistance \( R_V \).

The equivalent resistance \( R_p \) is the result of the parallel combination of \( R_1 = 100 \, \Omega \) and \( R_V \).

\[ R_p = \frac{R_1 \times R_V}{R_1 + R_V} \]

Substitute the known values:

\[ 50 = \frac{100 \times R_V}{100 + R_V} \]

Final Computation & Result:

Solve the equation for \( R_V \):

\[ 50(100 + R_V) = 100 R_V \] \[ 5000 + 50 R_V = 100 R_V \] \[ 5000 = 100 R_V - 50 R_V \] \[ 5000 = 50 R_V \] \[ R_V = \frac{5000}{50} = 100 \, \Omega \]

The resistance of the voltmeter is 100 Ω.