For a vector field \( \mathbf{D} = \rho \cos^2 \phi a_{\rho} + z^2 \sin^2 \phi a_{\phi} \) in a cylindrical coordinate system \( (\rho, \phi, z) \) with unit vectors \( a_{\rho}, a_{\phi}, a_z \), the net flux of \( \mathbf{D} \) leaving the closed surface of the cylinder \( (\rho = 3, 0 \leq z \leq 2) \) (rounded off to two decimal places) is .
Show Hint
Correct Answer: 56.5
Solution and Explanation
Top Questions on Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
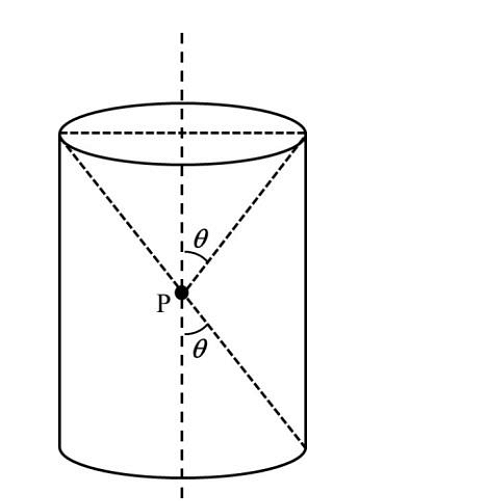
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in GATE EC exam
Eight students (P, Q, R, S, T, U, V, and W) are playing musical chairs. The figure indicates their order of position at the start of the game. They play the game by moving forward in a circle in the clockwise direction.
After the 1st round, the 4th student behind P leaves the game.
After the 2nd round, the 5th student behind Q leaves the game.
After the 3rd round, the 3rd student behind V leaves the game.
After the 4th round, the 4th student behind U leaves the game.
Who all are left in the game after the 4th round?
Here are two analogous groups, Group-I and Group-II, that list words in their decreasing order of intensity. Identify the missing word in Group-II.
Abuse \( \rightarrow \) Insult \( \rightarrow \) Ridicule
__________ \( \rightarrow \) Praise \( \rightarrow \) Appreciate
- A full adder and an XOR gate are used to design a digital circuit with inputs \( X, Y, Z \), and output \( F \), as shown below. The input \( Z \) is connected to the carry-in input of the full adder.
If the input \( Z \) is set to logic ‘1’, then the circuit functions as _________ with \( X \) and \( Y \) as inputs.- GATE EC - 2025
- Digital Circuits
Consider a system represented by the block diagram shown below. Which of the following signal flow graphs represent(s) this system? Choose the correct option(s).

- GATE EC - 2025
- Fourier series
- Consider a non-negative function \( f(x) \) which is continuous and bounded over the interval [2, 8]. Let \( M \) and \( m \) denote, respectively, the maximum and the minimum values of \( f(x) \) over the interval. Among the combinations of \( \alpha \) and \( \beta \) given below, choose the one(s) for which the inequality \[ \beta \leq \int_2^8 f(x) \, dx \leq \alpha \] is guaranteed to hold.
- GATE EC - 2025
- Calculus