An equation of a plane parallel to the plane \(x-2y+2z-5=0\) and at a unit distance from the origin is?
Solution and Explanation
The correct answer is \(x-2y+2z-3=0.\)
Let an equation of a plane parallel to the plane \(x−2y+2z−5=0\) be \(x−2y+2z+k=0\ \ \ ...(i)\)
Perpendicular distance from O(0,0,0) to (1) is 1
\(\frac{|k|}{\sqrt{1+4+4}}=1\)
\(⇒|k|=3\)
\(⇒k=+3\ \ or−3\)
\(∴x−2y+2z−3=0\)
Top Questions on Distance of a Point from a Plane
- The square of the distance of the point \(\left( \frac{15}{7}, \frac{32}{7}, 7 \right)\) from the line \(\frac{x+1}{3} = \frac{y+3}{5} = \frac{z+5}{7}\) in the direction of the vector \(\mathbf{i} + 4\mathbf{j} + 7\mathbf{k}\) is:
- JEE Main - 2025
- Mathematics
- Distance of a Point from a Plane
- If $ z_1 = 2 + 3i $, $ z_2 = 4 - 5i $, and $ z_3 $ are three points in the Argand plane such that $ 5z_1 + xz_2 + yz_3 = 0 $ (where $ x, y \in \mathbb{R} $) and $ z_3 $ is the midpoint of the line segment joining the points $ z_1 $ and $ z_2 $, then find $ x + y $.
- AP EAPCET - 2023
- Mathematics
- Distance of a Point from a Plane
For \(a, b \in \mathbb{Z}\) and \(|a - b| \leq 10\), let the angle between the plane \(P: ax + y - z = b\) and the line \(L: x - 1 = a - y = z + 1\) be \(\cos^{-1}\left(\frac{1}{3}\right)\). If the distance of the point \((6, -6, 4)\) from the plane \(P\) is \(3\sqrt{6}\), then \(a^4 + b^2\) is equal to:
- JEE Main - 2023
- Mathematics
- Distance of a Point from a Plane
Let P₁ be the plane 3x-y-7z = 11 and P₂ be the plane passing through the points (2,-1,0), (2,0,-1), and (5,1,1). If the foot of the perpendicular drawn from the point (7,4,-1) on the line of intersection of the planes P₁ and P₂ is (α, β, γ), then a + ẞ+ y is equal to
- JEE Main - 2023
- Mathematics
- Distance of a Point from a Plane
- Let \(\lambda_1, \lambda_2\) be the values of \(\lambda\) for which the points \((1, \lambda, \frac{1}{2})\) and \((-2, 0, 1)\) are at equal distance from the plane \(2x + 3y - 6z + 7 = 0\). If \(\lambda_1 > \lambda_2\), then the distance of the point \((1 - \lambda_2, \lambda_2, \lambda_1)\) from the line \(\frac{x-5}{1} = \frac{y-1}{2} = \frac{z+7}{2}\) is:
- JEE Main - 2023
- Mathematics
- Distance of a Point from a Plane
Questions Asked in JEE Main exam
- For a reaction, $$ {N}_2{O}_5(g) \rightarrow 2{NO}_2(g) + \frac{1}{2} {O}_2(g) $$ in a constant volume container, no products were present initially. The final pressure of the system when 50% of the reaction gets completed is:
- JEE Main - 2025
- Chemical Reactions
- If the image of the point $ P(1, 0, 3) $ in the line joining the points $ A(4, 7, 1) $ and $ B(3, 5, 3) $ is $ Q(\alpha, \beta, \gamma) $, then $ \alpha + \beta + \gamma $ is equal to:
- JEE Main - 2025
- 3D Geometry
Among the following cations, the number of cations which will give characteristic precipitate in their identification tests with
\(K_4\)[Fe(CN)\(_6\)] is : \[ {Cu}^{2+}, \, {Fe}^{3+}, \, {Ba}^{2+}, \, {Ca}^{2+}, \, {NH}_4^+, \, {Mg}^{2+}, \, {Zn}^{2+} \]- JEE Main - 2025
- Qualitative Analysis
A solution of aluminium chloride is electrolyzed for 30 minutes using a current of 2A. The amount of the aluminium deposited at the cathode is _________
- JEE Main - 2025
- Electrolysis
If \( z \) is a complex number and \( k \in \mathbb{R} \), such that \( |z| = 1 \), \[ \frac{2 + k^2 z}{k + \overline{z}} = kz, \] then the maximum distance from \( k + i k^2 \) to the circle \( |z - (1 + 2i)| = 1 \) is:
- JEE Main - 2025
- Complex numbers
Concepts Used:
Distance of a Point from a Plane
The shortest perpendicular distance from the point to the given plane is the distance between point and plane. In simple terms, the shortest distance from a point to a plane is the length of the perpendicular parallel to the normal vector dropped from the particular point to the particular plane. Let's see the formula for the distance between point and plane.
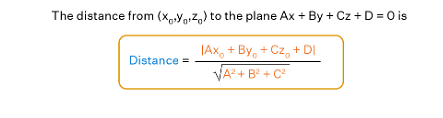
Read More: Distance Between Two Points