What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Solution and Explanation
All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.
Top Questions on Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
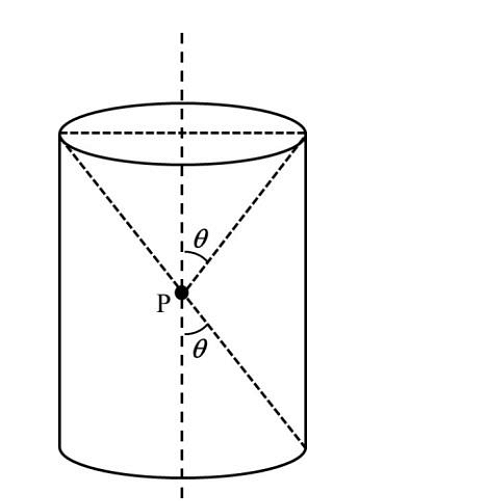
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in CBSE CLASS XII exam
If vector \( \mathbf{a} = 3 \hat{i} + 2 \hat{j} - \hat{k} \) \text{ and } \( \mathbf{b} = \hat{i} - \hat{j} + \hat{k} \), then which of the following is correct?
- Find the value of $x$, if \[ \begin{bmatrix} 1 & 3 & 2 \\ 2 & 5 & 1 \\ 15 & 3 & 2 \end{bmatrix} \begin{bmatrix} 1 \\ x \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \]
- Two point charges of \( -5\,\mu C \) and \( 2\,\mu C \) are located in free space at \( (-4\,\text{cm}, 0) \) and \( (6\,\text{cm}, 0) \) respectively.
(a) Calculate the amount of work done to separate the two charges at infinite distance.
(b) If this system of charges was initially kept in an electric field \[ \vec{E} = \frac{A}{r^2}, \text{ where } A = 8 \times 10^4\, \text{N}\,\text{C}^{-1}\,\text{m}^2, \] calculate the electrostatic potential energy of the system.- CBSE CLASS XII - 2025
- Electrostatics
- 4,000 shares of ₹ 10 each were forfeited for non-payment of second and final call money of ₹ 2 per share. The minimum amount that the company must collect at the time of reissue of these shares will be :
- CBSE CLASS XII - 2025
- Accounting for Share Capital
- If $y = a \cos(\log x) + b \sin(\log x)$, then $x^2y'' + xy'1$ is:
- CBSE CLASS XII - 2025
- Continuity and differentiability