Question:
Find the distance from a point of charge of magnitude \(5 \times 10^{-9} C\), where the electric potential is \(50 V\)
Find the distance from a point of charge of magnitude \(5 \times 10^{-9} C\), where the electric potential is \(50 V\)
Updated On: Jul 5, 2024
- 90 cm
- 70 cm
- 60 cm
- 50 cm
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
The correct option is (A): 90 cm
Was this answer helpful?
1
0
Top Questions on Electric Potential And Potential Difference
- A thin spherical shell is charged by some source. The potential difference between the two points C and P (in V) shown in the figure is:
(Take \(\frac{1}{4}\pi\epsilon_0 = 9 × 109\)\(\frac{1}{4\pi\epsilon_0}=9\times10^9\) SI units)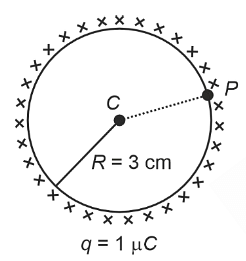
- NEET (UG) - 2024
- Physics
- Electric Potential And Potential Difference
- Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
- What will be potential and field due to a dipole of dipole moment 4.5×10-10 cm at a distance from 1 m from the center of the dipole along its axis?
- CUET (PG) - 2023
- Physics
- Electric Potential And Potential Difference
Choose correct graph of electric potential for uniformly charged hollow sphere.
- JEE Main - 2023
- Physics
- Electric Potential And Potential Difference
- For the network shown below, the value of VB– VA is ________V.
- JEE Main - 2022
- Physics
- Electric Potential And Potential Difference
View More Questions
Questions Asked in JEE Main exam
- If \(f(x) - f(y) = ln\bigg(\frac{x}{y}\bigg) +x-y\), then find \(\sum^{20}_{k=1}f'\bigg(\frac{1}{k^2}\bigg)\)
- JEE Main - 2024
- Functions
- Given below are two statements :
Statement I : The higher oxidation states are more stable down the group among transition elements unlike p-block elements.
Statement II : Copper can not liberate hydrogen from weak acids.
In the light of the above statements, choose the correct answer from the options given below- JEE Main - 2024
- Oxidation Number And Oxidation State
- Two thermodynamical processes are shown in the figure. The molar heat capacity for process \( A \) and \( B \) are \( C_A \) and \( C_B \). The molar heat capacity at constant pressure and constant volume are represented by \( C_P \) and \( C_V \), respectively. Choose the correct statement.
- JEE Main - 2024
- Thermodynamics
- A group of 40 students appeared in an examination of 3 subjects – Mathematics, Physics & Chemistry. It was found that all students passed in at least one of the subjects, 20 students passed in Mathematics, 25 students passed in Physics, 16 students passed in Chemistry, at most 11 students passed in both Mathematics and Physics, at most 15 students passed in both Physics and Chemistry, at most 15 students passed in both Mathematics and Chemistry. The maximum number of students passed in all the three subjects is ________.
- JEE Main - 2024
- Set Theory
- If \(4 cos\ θ + 5 sin\ θ = 1\), then all possible values of \(tan\ θ\), is/are
Where, \(θ∈(-\frac \pi2,\frac \pi2)\)- JEE Main - 2024
- Some Applications of Trigonometry
View More Questions